题目内容
如图所示，在P点有一个线状发光器绕发光器上的某一点为轴在纸面内以角速度ω逆时针匀速转动，发光器发出一束光线入射到下方的两面平行玻璃砖的上表面，P与玻璃砖的上表面距离为H，当光线与玻璃砖的表面成45°时，在玻璃砖内的光线与法线夹角为30°，求（1）玻璃砖的折射率．
（2）该时刻光线在玻璃砖上表面的入射点移动的速度．
【答案】分析：（1）已知光线与玻璃砖的表面成45°时，在玻璃砖内的光线与法线夹角为30°，由折射定律求出折射率．
（2）入射点沿表面向左移动，将该速度v沿光线和垂直光线方向分解分别为v1和v2，根据圆周运动的规律求出v2，再求解光线在玻璃砖上表面的入射点移动的速度v．
解答：解：（1）根据折射定律得：
（2）入射点沿表面向左移动，将该速度v沿光线和垂直光线方向分解分别为v1和v2
得：
而：v2=ω?
H
得：v=2ωH
答：（1）玻璃砖的折射率是1.414．
（2）该时刻光线在玻璃砖上表面的入射点移动的速度为2ωH．
点评：本题第1问是基础题，已知入射角和折射角，由折射定律求解折射率．第2问运用运动的分解法进行求解，此题与通过滑轮用绳拉船的问题类似，将船速分解为沿绳和垂直绳两个方向，研究船速与绳速的关系．
（2）入射点沿表面向左移动，将该速度v沿光线和垂直光线方向分解分别为v1和v2，根据圆周运动的规律求出v2，再求解光线在玻璃砖上表面的入射点移动的速度v．
解答：解：（1）根据折射定律得：
（2）入射点沿表面向左移动，将该速度v沿光线和垂直光线方向分解分别为v1和v2
得：
而：v2=ω?
H得：v=2ωH
答：（1）玻璃砖的折射率是1.414．
（2）该时刻光线在玻璃砖上表面的入射点移动的速度为2ωH．
点评：本题第1问是基础题，已知入射角和折射角，由折射定律求解折射率．第2问运用运动的分解法进行求解，此题与通过滑轮用绳拉船的问题类似，将船速分解为沿绳和垂直绳两个方向，研究船速与绳速的关系．
练习册系列答案
相关题目
（2009?宁夏）如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；在x轴下方有一匀强磁场，磁场方向与纸面垂直．一质量为m、电荷量为-q（q＞0）的粒子以平行于x轴的速度从y轴上的P点处射入电场，在x轴上的Q点处进入磁场，并从坐标原点O离开磁场．粒子在磁场中的运动轨迹与y轴交于M点．已知OP=l，OQ=2
如图所示，在P点有一个线状发光器绕发光器上的某一点为轴在纸面内以角速度ω逆时针匀速转动，发光器发出一束光线入射到下方的两面平行玻璃砖的上表面，P与玻璃砖的上表面距离为H，当光线与玻璃砖的表面成45°时，在玻璃砖内的光线与法线夹角为30°，求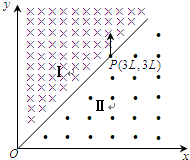
如图所示，在空间中有一坐标系oxy，其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ．直线OP是它们的边界．区域Ⅰ中的磁感应强度为2B，方向垂直纸面向内，区域Ⅱ中的磁感应强度为B，方向垂直纸面向外，边界上的P点坐标为（3L，3L）．一质量为m，电荷量为+q的粒子从P点平行于y轴正方向以速度v0=