题目内容
18.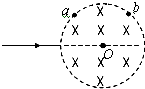 圆形区域内有如图所示的匀强磁场,一束相同荷质比的带电粒子对准圆心O射入,分别从a、b两点射出,则从b点射出的粒子( )
圆形区域内有如图所示的匀强磁场,一束相同荷质比的带电粒子对准圆心O射入,分别从a、b两点射出,则从b点射出的粒子( )| A. | 匀强磁场对b做的功较多 | B. | 运动半径较小 | ||
| C. | 速率较小 | D. | 在磁场中的运动时间较短 |
分析 洛伦兹力对带电粒子不做功.荷质比相同的带电粒子,以不同的速率垂直进入匀强磁场中,运动半径的不同,导致运动轨迹也不同,运动轨迹对应的半径越大,则粒子的速率也越大.而运动周期它们均一样,但运动时间却由圆弧对应的圆心角决定.
解答 解:A、带电粒子在匀强磁场中受到洛伦兹力作用,而洛伦兹方向总与粒子的速度方向垂直,对粒子不做功,故A错误.
BC、由洛伦兹力提供向心力,得:qvB=m$\frac{{v}^{2}}{r}$解得:r=$\frac{mv}{qB}$,可知两个粒子的荷质比相同,则轨迹半径与速率成正比,结合几何运动径迹可知,从b点射出的粒子运动的半径较大,其运动速率较大,故B、C错误;
D、由图可以看出a粒子偏转角较大,b粒子偏转角较小,粒子在磁场中运动周期为 T=$\frac{2πm}{qB}$,由于荷质比相同,周期与速率无关,仅由轨迹所对的圆心角决定,故b点射出的粒子运动时间较短,故D正确;
故选:D.
点评 本题关键是结合圆的对称性,运用洛伦兹力提供向心力列式分析计算.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
9. “嫦娥一号”探月卫星沿地月转移轨道直奔月球,在距月球表面200km的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法正确的是( )
“嫦娥一号”探月卫星沿地月转移轨道直奔月球,在距月球表面200km的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法正确的是( )
 “嫦娥一号”探月卫星沿地月转移轨道直奔月球,在距月球表面200km的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法正确的是( )
“嫦娥一号”探月卫星沿地月转移轨道直奔月球,在距月球表面200km的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法正确的是( )| A. | 卫星在轨道Ⅲ上运动的速度大于月球的第一宇宙速度 | |
| B. | 卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上长 | |
| C. | 卫星在轨道Ⅲ上运动到P点的加速度大于沿轨道Ⅰ运动到P点的加速度 | |
| D. | Ⅰ、Ⅱ、Ⅲ三种轨道运行相比较,卫星在轨道Ⅲ上运行的机械能最小 |
6. 如图甲所示的电路中M位以电动机,在滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表在0.2A以下时,电动机没有发生转动,各电表均为理想电表,以下判断正确的是( )
如图甲所示的电路中M位以电动机,在滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表在0.2A以下时,电动机没有发生转动,各电表均为理想电表,以下判断正确的是( )
 如图甲所示的电路中M位以电动机,在滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表在0.2A以下时,电动机没有发生转动,各电表均为理想电表,以下判断正确的是( )
如图甲所示的电路中M位以电动机,在滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表在0.2A以下时,电动机没有发生转动,各电表均为理想电表,以下判断正确的是( )| A. | 曲线MQ为电压表V2的读数随电流表读数变化的图象 | |
| B. | 电源E的内阻为2Ω | |
| C. | 电动机的最大输出功率为0.9W | |
| D. | 滑动变阻器的最大阻值为30Ω |
13. 封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度关T系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.由状态A变到状态D过程中( )(填写选项前的字母)
封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度关T系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.由状态A变到状态D过程中( )(填写选项前的字母)
 封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度关T系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.由状态A变到状态D过程中( )(填写选项前的字母)
封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度关T系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.由状态A变到状态D过程中( )(填写选项前的字母)| A. | 气体从外界吸收热量,内能减少 | |
| B. | 气体体积增大,单位时间内与器壁单位面积碰撞的分子数减少 | |
| C. | 气体温度升高,每个气体分子的动能都会增大 | |
| D. | 气体的密度不变 |
10. 在如图所示的电路中,电源的内电阻r不能忽略,其电动势E小于电容器C的耐压值.开关S原来是断开的,现闭合开关S,则在电路再次达到稳定的过程中,下列说法中正确的是( )
在如图所示的电路中,电源的内电阻r不能忽略,其电动势E小于电容器C的耐压值.开关S原来是断开的,现闭合开关S,则在电路再次达到稳定的过程中,下列说法中正确的是( )
 在如图所示的电路中,电源的内电阻r不能忽略,其电动势E小于电容器C的耐压值.开关S原来是断开的,现闭合开关S,则在电路再次达到稳定的过程中,下列说法中正确的是( )
在如图所示的电路中,电源的内电阻r不能忽略,其电动势E小于电容器C的耐压值.开关S原来是断开的,现闭合开关S,则在电路再次达到稳定的过程中,下列说法中正确的是( )| A. | 电阻R1两端的电压减小 | B. | 电容器C两端的电压增大 | ||
| C. | 电源两端的电压减小 | D. | 电容器C上所带的电量减小 |
7.关于同步卫星,下列说法不正确的是( )
| A. | 同步卫星的运动轨道平面一定与赤道平面重合 | |
| B. | 所有地球同步卫星到地心的距离都相同 | |
| C. | 所有地球同步卫星的质量都相同 | |
| D. | 同步卫星运行的线速度大小一定小于第一宇宙速度 |
8. 物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度、始终相对静止靠惯性沿固定斜面C向上做匀减速运动时,( )
物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度、始终相对静止靠惯性沿固定斜面C向上做匀减速运动时,( )
 物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度、始终相对静止靠惯性沿固定斜面C向上做匀减速运动时,( )
物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度、始终相对静止靠惯性沿固定斜面C向上做匀减速运动时,( )| A. | A受到B的摩擦力沿斜面方向向上 | |
| B. | A受到B的摩擦力沿斜面方向向下 | |
| C. | A、B之间是否存在摩擦力取决于A、B表面的性质 | |
| D. | A、B之间是否存在摩擦力取决于A、C表面的性质 |
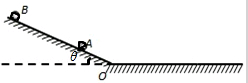 如图所示,斜面光滑且倾角θ=30°,斜面与水平面圆滑对接,已知两个完全一样的小滑块A、B静止在斜面上的初始位置离斜面底端O点的距离分别为LA=L,LB=4L,水平面粗糙且小滑块之间的动摩擦因数均为μ,忽略小滑块在经过O处得能量损失,重力加速度大小为g,求:
如图所示,斜面光滑且倾角θ=30°,斜面与水平面圆滑对接,已知两个完全一样的小滑块A、B静止在斜面上的初始位置离斜面底端O点的距离分别为LA=L,LB=4L,水平面粗糙且小滑块之间的动摩擦因数均为μ,忽略小滑块在经过O处得能量损失,重力加速度大小为g,求: (1)有一多用电表,它的欧姆刻度线中心刻度值是15,当用R×10档去测量某待测电阻(阻值约为1000Ω)时,指针偏转角度较小.为了减小测量误差,应该重新测量.其实验步骤的顺序是DFEBA(填写字母)
(1)有一多用电表,它的欧姆刻度线中心刻度值是15,当用R×10档去测量某待测电阻(阻值约为1000Ω)时,指针偏转角度较小.为了减小测量误差,应该重新测量.其实验步骤的顺序是DFEBA(填写字母)