题目内容
10. 如图所示,在水平地面上固定着一个倾角θ=37°、表面光滑且足够长的斜面体,物体A以v1=6m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出.如果当A上滑到速度为0时恰好被B物体击中.(A、B均可看作质点,sin37°=0.6,cos37°=0.8.g取10m/s2.)求:
如图所示,在水平地面上固定着一个倾角θ=37°、表面光滑且足够长的斜面体,物体A以v1=6m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出.如果当A上滑到速度为0时恰好被B物体击中.(A、B均可看作质点,sin37°=0.6,cos37°=0.8.g取10m/s2.)求:(1)物体A上滑到最高点所用的时间t
(2)物体B抛出时的初速度v2
(3)物体A、B间初始位置的高度差h.
分析 (1)对物体A进行受力分析,可以根据牛顿第二定律求出A上滑的加速度,再由匀变速直线运动的速度公式可以求得运动的时间;
(2)由几何关系得出B平抛运动的水平位移,结合时间求出初速度的大小.
(3)物体A、B间初始位置的高度差等于A上升的高度和B下降的高度的和,A上升的高度可以由A的运动求出,B下降的高度就是自由落体的竖直位移.
解答 解(1)根据牛顿第二定律得,A上滑的加速度大小 a=gsin37°=6m/s2.
运动的时间 t=$\frac{{v}_{1}}{a}$=$\frac{6}{6}$s=1s.
(2)A物体运动的位移 xA=$\frac{{v}_{1}^{2}}{2a}$=$\frac{{6}^{2}}{2×6}$m=3m.
则B平抛运动的水平位移 x=xAcos37°=v2t
解得B抛出的初速度 v2=2.4m/s.
(3)B平抛运动下落的高度 h1=$\frac{1}{2}$gt2=$\frac{1}{2}$×10×1m=5m.
A上升的高度 h2=xAsin37°=1.8m
则AB初始位置的高度差△h=h1+h2=6.8m.
答:
(1)物体A上滑到最高点所用的时间t为1s.
(2)物体B抛出时的初速度为2.4m/s.
(3)物体A、B间初始位置的高度差h为6.8m.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住与A运动的时间相等,水平位移相等,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
1.下列说法不正确的是( )
| A. | 我们看到水中的筷子弯折是光的折射现象 | |
| B. | 在光导纤维束内传送图象是利用光的全反射现象 | |
| C. | 水中的气泡特别明亮是光的干涉现象 | |
| D. | 小孔成像是利用光的直线传播 |
18.当两个分子间的距离r=r0时,分子处于平衡状态,设r1<r0<r2,则当两个分子间的距离由r1变到r2的过程中,有可能发生的变化情况是( )
| A. | 分子力先减小后增加 | B. | 分子力先减小再增加然后再减小 | ||
| C. | 分子势能先减小后增加 | D. | 分子势能先增大后减小 |
15.铁路弯道处,内外轨组成的斜面与水平地面倾角为θ,当火车以某一速度v通过该弯道时,内、外轨恰不受侧压力作用,则下面说法正确的是( )
| A. | 转弯半径R=$\frac{{v}^{2}}{gsinθ}$ | |
| B. | 若火车速度大于v时,外轨将受到侧压力作用,其方向平行轨道平面向外 | |
| C. | 若火车速度小于v时,外轨将受到侧压力作用,其方向平行轨道平面向内 | |
| D. | 当火车质量改变时,安全速率也将改变 |
2. 如图所示是简式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )
如图所示是简式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )
 如图所示是简式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )
如图所示是简式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )| A. | 此时千斤顶对汽车的支持力为2.0×105N | |
| B. | 若继续原方向摇动手把,千斤顶对汽车的支持力将减小 | |
| C. | 若继续原方向摇动手把,两臂受到的压力将增大 | |
| D. | 若继续原方向摇动手把,两臂受到的压力将减小 |
20.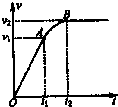 质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
 质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )| A. | 0-t1时间内,汽车牵引力的数值为m$\frac{v_1}{t_1}$ | |
| B. | t1-t2时间内,汽车的功率等于(m$\frac{{v}_{1}}{{t}_{1}}$+Ff)v2 | |
| C. | tl-t2时间内,汽车的平均速率小于$\frac{{v}_{1}+{v}_{2}}{2}$v2 | |
| D. | 汽车运动的最大速率v2=($\frac{m{v}_{1}}{{F}_{f}{t}_{1}}$+1)v1 |

 如图所示为一输电系统,A地有一台升压变压器,B地有一台匝数比为10:1的降压变压器,降压变压器副线圈上的电流为100A,输出功率是12kW,A、B两地输电线的电阻是20Ω,求:
如图所示为一输电系统,A地有一台升压变压器,B地有一台匝数比为10:1的降压变压器,降压变压器副线圈上的电流为100A,输出功率是12kW,A、B两地输电线的电阻是20Ω,求: