题目内容
12. 粒子回旋加速器的工作原理如图所示,置于真空中的D形金属盒的半径为R,两金属盒间的狭缝很小,磁感应强度为B的匀强磁场与金属盒盒面垂直,高频交流电的频率为f,加速电场的电压为U,若中心粒子源处产生的质子质量为m,电荷量为+e,在加速器中被加速.不考虑相对论效应,则下列说法正确是( )
粒子回旋加速器的工作原理如图所示,置于真空中的D形金属盒的半径为R,两金属盒间的狭缝很小,磁感应强度为B的匀强磁场与金属盒盒面垂直,高频交流电的频率为f,加速电场的电压为U,若中心粒子源处产生的质子质量为m,电荷量为+e,在加速器中被加速.不考虑相对论效应,则下列说法正确是( )| A. | 不改变磁感应强度B和交流电的频率f,该加速器也可加速α粒子 | |
| B. | 质子第二次和第一次经过D形盒间狭缝后轨道半径之比为$\sqrt{2}$:l | |
| C. | 质子被加速后的最大速度不能超过2πRf | |
| D. | 加速的粒子获得的最大动能随加速电压U的增大而增大 |
分析 回旋加速器运用电场加速磁场偏转来加速粒子,根据洛伦兹力提供向心力可以求出粒子的最大速度,从而求出最大动能.在加速粒子的过程中,电场的变化周期与粒子在磁场中运动的周期相等.
解答 解:A、带电粒子在磁场中运动的周期与加速电场的周期相等,根据T=$\frac{2πm}{qB}$知,换用α粒子,粒子的比荷变化,周期变化,回旋加速器需改变交流电的频率才能加速α粒子.故A错误.
B、粒子在加速电场中做匀加速运动,在磁场中做匀速圆周运动,根据v=$\sqrt{2ax}$ 知,质子第二次和第一次经过D形盒狭缝的速度比为$\sqrt{2}$:1,根据r=$\frac{mv}{qB}$,则半径比为$\sqrt{2}$:1.故B正确.
C、质子出回旋加速器的速度最大,此时的半径为R,则v=$\frac{2πR}{T}$=2πRf.所以最大速度不超过2πfR.故C正确.
D、根据qvB=m$\frac{{v}^{2}}{R}$,知v=$\frac{BRq}{m}$,则最大动能EKm=$\frac{1}{2}$mv2=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$.与加速的电压无关.故D错误.
故选:BC
点评 解决本题的关键知道回旋加速器电场和磁场的作用,知道最大动能与什么因素有关,以及知道粒子在磁场中运动的周期与电场的变化的周期相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.我国计划在2017年12月发射“嫦娥五号”探测器,主要是完成月面取样返回任务,设探测器在离月面高度为h的轨道上绕月做匀速圆周运动时,周期为T,已知月球表面重力加速度为g0,月球半径为R,万有引力常量为G,根据以上信息可求出( )
| A. | 探测器绕月运行的速度为$\frac{2πR}{T}$ | B. | 月球的第一宇宙速度为$\sqrt{R{g}_{0}}$ | ||
| C. | 月球的质量为$\frac{{R}^{2}{g}_{0}}{G}$ | D. | 月球的平均密度为$\frac{3π}{G{T}^{2}}$ |
3. 如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )
如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )
 如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )
如图所示,光滑水平面上存有界匀强磁场,磁感应强度为B,质量为m边长为a的正方形线框ABCD斜向穿进磁场,当AC刚进入磁场时速度为v,方向与磁场边界成45°,若线框的总电阻为R,则( )| A. | 线框穿进磁场过程中,框中电流的方向为DCBA | |
| B. | AC刚进入磁场时线框中感应电流表为$\frac{{\sqrt{2}Bav}}{R}$ | |
| C. | AC刚进入磁场时线框所受安培力为$\frac{{\sqrt{2}{B^2}{a^2}v}}{R}$ | |
| D. | 此时CD两端电压为$\frac{3}{4}Bav$ |
17. 如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )
如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )
 如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )
如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )| A. | $\frac{mg}{2}$ | B. | $\frac{\sqrt{3}mg}{3}$ | C. | mg | D. | $\sqrt{3}$mg |
2.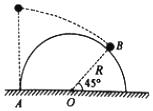 如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为45°,重力加速度为g,则小球抛出时的初速度为( )
如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为45°,重力加速度为g,则小球抛出时的初速度为( )
 如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为45°,重力加速度为g,则小球抛出时的初速度为( )
如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为45°,重力加速度为g,则小球抛出时的初速度为( )| A. | $\sqrt{\frac{\sqrt{2}}{2}gR}$ | B. | $\sqrt{(\frac{\sqrt{2}}{2}+1)gR}$ | C. | $\sqrt{(1-\frac{\sqrt{2}}{2})gR}$ | D. | $\sqrt{(\sqrt{2}-1)gR}$ |
 如图示,光滑的U型导轨形成一个倾角为30°的斜面,导轨的水平间距为l=10cm,在斜面上有垂直斜面向上的匀强磁场,磁感应强度B=20T,一质量为m=2kg的导体棒在导轨上由静止释放,导体棒的电阻R=2Ω,导轨电阻不计,当小球沿斜面下滑S=6m时,导体棒获得最大速度.求
如图示,光滑的U型导轨形成一个倾角为30°的斜面,导轨的水平间距为l=10cm,在斜面上有垂直斜面向上的匀强磁场,磁感应强度B=20T,一质量为m=2kg的导体棒在导轨上由静止释放,导体棒的电阻R=2Ω,导轨电阻不计,当小球沿斜面下滑S=6m时,导体棒获得最大速度.求 如图所示,MN右侧有底边长为L高为L的等腰三角形匀强磁场区域(边缘磁场忽略不计),上边界与MN垂直.现有一高为L宽为$\frac{L}{2}$的长方形导体框,从MN左侧垂直于MN匀速向右运动.导体框穿过磁场过程中感应电流I随距离x变化的图象正确的是(取逆时针电流为正)( )
如图所示,MN右侧有底边长为L高为L的等腰三角形匀强磁场区域(边缘磁场忽略不计),上边界与MN垂直.现有一高为L宽为$\frac{L}{2}$的长方形导体框,从MN左侧垂直于MN匀速向右运动.导体框穿过磁场过程中感应电流I随距离x变化的图象正确的是(取逆时针电流为正)( )




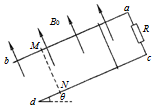 如图所示,ab、cd为间距d=1m的光滑倾斜金属导轨,与水平面的夹角θ=37°,导轨电阻不计,a、c间连接电阻R=2.4Ω.空间存在磁感应强度B0=2T的匀强磁场,方向垂直于导轨平面向上.将一根金属棒放置在导轨上距ac为x0=0.5m处,其质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动过程中始终与ac平行且与导轨接触良好.已知当金属棒从初始位置向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
如图所示,ab、cd为间距d=1m的光滑倾斜金属导轨,与水平面的夹角θ=37°,导轨电阻不计,a、c间连接电阻R=2.4Ω.空间存在磁感应强度B0=2T的匀强磁场,方向垂直于导轨平面向上.将一根金属棒放置在导轨上距ac为x0=0.5m处,其质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动过程中始终与ac平行且与导轨接触良好.已知当金属棒从初始位置向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,sin37°=0.6,cos37°=0.8,g取10m/s2.求: