题目内容
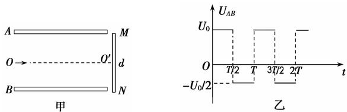
如图甲所示，水平放置足够长的平行金属导轨，左右两端分别接有一个阻值为R的电阻，匀强磁场与导轨平面垂直，质量m = 0.1 kg、电阻r =
的金属棒置于导轨上，与导轨垂直且接触良好。现用一拉力F =（0.3+0.2t）N作用在金属棒上，经过2s后撤去F，再经过0.55s金属棒停止运动。图乙所示为金属棒的v–t图象，g = 10m/s2。求：
1.金属棒与导轨之间的动摩擦因数；
2.整个过程中金属棒运动的距离；
3.从撤去F到金属棒停止的过程中，每个电阻R上产生的焦耳热。
1.
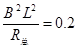
2.
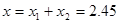m
3.
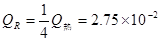J
【解析】(1)在0-2s这段时间内，根据牛顿第二定律 有
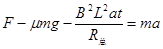（2分）
由图可知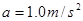 
（1分）
又因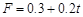 
联立解得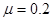 
，
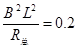（1分）
（1分）
(2) 在0--2s这段时间内的位移为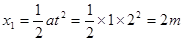
（1分）
设棒在2---2.55s时间内的位移为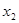
，
棒在 t时刻，根据牛顿第二定律 有
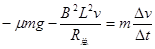（1分）
在t到t+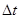
（
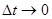）时间内
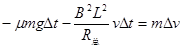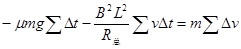（1分）
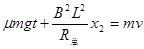（1分）
（1分）
代入数据得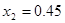 
m
整个过程中金属棒运动的距离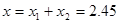m （1分）
（3）从撤去拉力到棒停止的过程中，根据能量守恒定律 有
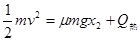（2分）
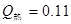J
（1分）
每个电阻R上产生的焦耳热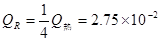J （2分）
天天向上一本好卷系列答案
小学生10分钟应用题系列答案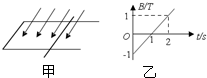
如图甲所示，水平放置的平行金属导轨连接一个平行板电容器C和电阻R，导体棒MN放在导轨上且接触良好，整个装置放于垂直导轨平面的磁场中，磁感应强度B的变化情况如图乙所示（图示磁感应强度方向为正），MN始终保持静止，则0～t2时间（ ）
如图甲所示，水平放置的平行金属板A和B间的距离为d，金属板长L=2
如图甲所示，水平放置的U形金属导轨宽度为25cm，其电阻不计．阻值为2?的金属棒与导轨垂直放置．金属棒与导轨左端相距40cm．匀强磁场与水平面的夹角为30°斜向下，从t=0时刻起磁感应强度随时间的变化如图乙所示．已知在0～2s内金属棒始终处于静止状态．则下列说法中正确的是（ ）| A、在t=0时，金属棒所受安培力为零 | B、在t=1s时，金属棒所受安培力为零 | C、在t=0与t=2s时，金属棒所受安培力大小相等 | D、在t=0到t=2s时间内流过金属棒横截面积的电荷量为0.05C |