题目内容
一根劲度系数为k的轻弹簧水平放置,一端固定,另一端连接一个质量为m的物块,放在水平桌面上,现将物块沿弹簧长度方向拉离平衡位置O,到x处静止释放,此后物体在平衡位置附近来回运动,由于摩擦,振动不断衰减,当物块第n次速度为零时,恰好停在平衡位置处,求物体与桌面间的摩擦因数.
答案:
解析:
解析:
|
由于摩擦阻力的存在,物体的振动为阻尼振动,不过它的阻力大小却保持不变,属常量阻力下的振动,因最后物体静止于平衡位置处,若摩擦因数已知,则第n-1次速度为零的位置确定,以此从后往前推,可确定出释放的初始位置,从而想到用逆推法可解本题. 设物块从距平衡位置为x0处从静止开始运动,以后各次速度为零时到平衡位置的距离分别为x1、x2、……xn-2、xn-1(xn=0)逐项应用动能定理有:
……
从以上方程分别可得
x0=x1+
x1=x2+ …… xn-2=xn-1+
xn-1= 各项相加得
x0= 即
μ= |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
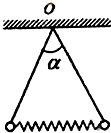 如图所示,两个质量都为m的完全相同的小球,分别用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止时弹簧位于水平方向,两根细线的夹角为α,则以下说法正确的是( )
如图所示,两个质量都为m的完全相同的小球,分别用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止时弹簧位于水平方向,两根细线的夹角为α,则以下说法正确的是( )A、弹簧的长度压缩了
| ||||
B、弹簧的长度压缩了
| ||||
C、弹簧受到的合力为2mgtan(
| ||||
| D、弹簧的弹力大小为2mgtanα |
 如图所示,两块质量分别为m1、m2的木板,被一根劲度系数为k的轻弹簧连在一起,并在m1板上加压力F为了使得撤去F后,m1跳起时恰好能带起m2板,则所加压力F的最小值为( )
如图所示,两块质量分别为m1、m2的木板,被一根劲度系数为k的轻弹簧连在一起,并在m1板上加压力F为了使得撤去F后,m1跳起时恰好能带起m2板,则所加压力F的最小值为( ) (2010?厦门二模)如图所示,A、B两球完全相同,质量为m,用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为θ.则弹簧的长度被压缩了( )
(2010?厦门二模)如图所示,A、B两球完全相同,质量为m,用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为θ.则弹簧的长度被压缩了( )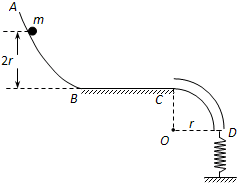 如图,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接内壁光滑、半径为r的细圆管CD,管口D端正下方直立一根劲度系数为k的轻弹簧,轻弹簧下端固定,上端恰好与管口D端齐平.质量为m的小球在曲面上距BC的高度为2r处从静止开始下滑,进入管口C端时与管壁间恰好无作用力,通过CD后压缩弹簧,在压缩弹簧过程中速度最大时弹簧的弹性势能为EP,已知小球与BC间的动摩擦因数μ=0.5.求:
如图,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接内壁光滑、半径为r的细圆管CD,管口D端正下方直立一根劲度系数为k的轻弹簧,轻弹簧下端固定,上端恰好与管口D端齐平.质量为m的小球在曲面上距BC的高度为2r处从静止开始下滑,进入管口C端时与管壁间恰好无作用力,通过CD后压缩弹簧,在压缩弹簧过程中速度最大时弹簧的弹性势能为EP,已知小球与BC间的动摩擦因数μ=0.5.求: