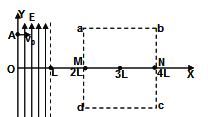题目内容
【题目】如图所示，两平行带电金属板M、N长度及间距均为2R，在两板间半径为R的圆形区域内有磁感应强度方向垂直纸面向里、大小为B的匀强磁场，两板及左右侧边缘连线均与磁场边界恰好相切。一质量为m、电荷量为+q的带电粒子沿两板间中心线O1O2，从左侧O1点以初速度v0射入，沿直线通过圆形磁场区域，从右侧O2点射出，不计粒子重力。求：
（1）M、N板的带电性质及两板间电压U；
（2）若两极板不带电，保持磁场不变，粒子仍沿中心线O1O2从左侧O1点射入，欲使粒子能从两板间射出，则射入的初速度应满足的条件。
【答案】（1）2BRv0；（2）0＜v＜
或v＞
。
【解析】
（1）粒子进入两板间做匀速直线运动，即电场力与洛伦兹力等大反向，则可得M板带止电，N板带负电，根据平衡条件有
解得
（2）粒子从上极板的左侧边缘飞出，设粒子在磁场中做圆周运动的半径为r1，作出运动轨迹如图所示
由几何关系可得
由洛伦兹力提供向心力
解得
粒了从上极板的右侧边缘飞出，粒了在磁场中做圆周运动的半径为r2，由几何关系可得
同理可解得此时射入速度为
综上所述可得，欲使粒子从两板间射出，则射入的初速度满足的条件为
0＜v＜或v＞
练习册系列答案
名校课堂系列答案
相关题目
