题目内容
如图甲所示,用一水平外力F推着一个静止在倾角为θ的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10m/s2.根据图乙中所提供的信息可以计算出(sin37°=0.6)( )


| A、物体的质量 | B、斜面的倾角 | C、物体能静止在斜面上所施加的外力 | D、加速度为6m/s2时物体的速度 |
分析:对物体进行受力分析,根据牛顿第二定律求出物体加速度与拉力F的关系式,根据图线的斜率和截距可以求出物体的质量和倾角.
解答:解:物体受重力、拉力和支持力,根据牛顿第二定律a=
=
-gsinθ.图线的纵轴截距为-6m/s2,则gsinθ=6,解得斜面的倾角θ=37°.
图线的斜率:k=
=
=
,因为sinθ=0.6,则cosθ=0.8,所以m=2kg.
物体刚好静止在斜面上时,a=0,故a=
=0,
解得F=mgtanθ=15N;
故A、B、C正确,D错误.
故选:ABC
| Fcosθ-mgsinθ |
| m |
| Fcosθ |
| m |
图线的斜率:k=
| cosθ |
| m |
| 6-2 |
| 30-20 |
| 2 |
| 5 |
物体刚好静止在斜面上时,a=0,故a=
| Fcosθ-mgsinθ |
| m |
解得F=mgtanθ=15N;
故A、B、C正确,D错误.
故选:ABC
点评:解决本题的关键能够正确地进行受力分析,运用牛顿第二定律求解,以及能够从图线的斜率和截距获取信息.

练习册系列答案
相关题目
 如图甲所示.用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的 物体.逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取lOm/s2根据阁乙中所提供的信息不能计算出( )
如图甲所示.用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的 物体.逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取lOm/s2根据阁乙中所提供的信息不能计算出( )| A、斜面的倾角 | B、加速度为2m/s2时物体所受的合外力 | C、物体静止在斜面上所施加的最小外力 | D、加速度为4m/s2时物体的速度 |
如图甲所示,用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体,F随时间均匀增大,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10m/s2.根据图乙中所提供的信息可以计算出( )


| A、物体的质量 | B、斜面的倾角 | C、斜面的长度 | D、加速度为6m/s2时物体对斜面的压力是34N |
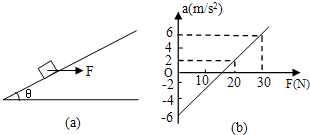 (2009?淄博二模)如图甲所示,用一水平力F拉着一个静止在固定斜面上的物体,斜面倾角为θ且光滑.现让F逐渐增大,物体加速度a随F变化的图象如图乙所示,若重力加速度g取10m/s2,根据图乙中所提供的信息可以计算出( )
(2009?淄博二模)如图甲所示,用一水平力F拉着一个静止在固定斜面上的物体,斜面倾角为θ且光滑.现让F逐渐增大,物体加速度a随F变化的图象如图乙所示,若重力加速度g取10m/s2,根据图乙中所提供的信息可以计算出( )