题目内容
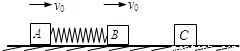
光滑水平面上,用弹簧相连接的质量均为2kg的A、B两物体都以v=6m/s速度向右运动,弹簧处于原长.质量为4kg的物体C静止在前方,如图所示,B与C发生碰撞后粘合在一起运动,求:①B、C碰撞刚结束时的瞬时速度;
②在以后的运动过程中,物体A是否会有速度等于零的时刻?试通过定量分析,说明你的理由.
【答案】分析:(1)根据动量守恒定律求出B、C碰刚结束时的瞬时速度.
(2)通过动量守恒定律求出物体A速度为零时,BC的速度大小,结合能量守恒求出弹簧的弹性势能,从而确定出A的速度能否为零.
解答:解:①设B、C碰撞后的瞬间速度为v1,根据动量守恒定律有
mBv=(mB+mC)v1
解得:v1=2m/s
②物体A会有速度等于零的时刻.说明理由如下:
设当A的速度为零时,B、C整体的速度为vBC,根据动量守恒定律有
mAv+mBv=(mB+mC)vBC
解得:vBC=4m/s
此时的弹性势能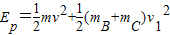 -
-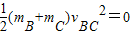
即当A的速度为零时,B、C整体的速度为4m/s,此时弹簧正好处于原长.
答:(1)B、C碰撞刚结束时的瞬时速度为2m/s.
(2)物体A会有速度等于零的时刻.
点评:本题考查了动量守恒定律和能量守恒定律的综合运用,关键是合理的选择研究的对象,难度中等,需加强这方面的训练.
(2)通过动量守恒定律求出物体A速度为零时,BC的速度大小,结合能量守恒求出弹簧的弹性势能,从而确定出A的速度能否为零.
解答:解:①设B、C碰撞后的瞬间速度为v1,根据动量守恒定律有
mBv=(mB+mC)v1
解得:v1=2m/s
②物体A会有速度等于零的时刻.说明理由如下:
设当A的速度为零时,B、C整体的速度为vBC,根据动量守恒定律有
mAv+mBv=(mB+mC)vBC
解得:vBC=4m/s
此时的弹性势能
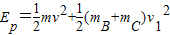 -
-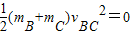
即当A的速度为零时,B、C整体的速度为4m/s,此时弹簧正好处于原长.
答:(1)B、C碰撞刚结束时的瞬时速度为2m/s.
(2)物体A会有速度等于零的时刻.
点评:本题考查了动量守恒定律和能量守恒定律的综合运用,关键是合理的选择研究的对象,难度中等,需加强这方面的训练.

练习册系列答案
相关题目
 光滑水平面上,用弹簧相连接的质量均为2kg的A、B两物体都以v0=6m/s速度向右运动,弹簧处于原长.质量为4kg的物体C静止在前方,如图所示,B与C发生碰撞后粘合在一起运动,在以后的运动中,求:
光滑水平面上,用弹簧相连接的质量均为2kg的A、B两物体都以v0=6m/s速度向右运动,弹簧处于原长.质量为4kg的物体C静止在前方,如图所示,B与C发生碰撞后粘合在一起运动,在以后的运动中,求: 如图所示,在光滑水平面上,用弹簧水平连接一斜面,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动.则( )
如图所示,在光滑水平面上,用弹簧水平连接一斜面,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动.则( ) 如图所示,在光滑水平面上,用弹簧水平连接一斜面,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动.当人沿斜面加速上升,则( )
如图所示,在光滑水平面上,用弹簧水平连接一斜面,弹簧的另一端固定在墙上,一人站在斜面上,系统静止不动.当人沿斜面加速上升,则( ) [物理-选修3-5]
[物理-选修3-5]