题目内容
静止在匀强磁场中的
Li核俘获一个速度为v0=7.7×104 m/s的中子而发生核反应
Li+
n→
H+
He，
He和中子的运动轨迹在与磁场垂直的平面内，若已知
He的速度为v2=2.0×104 m/s，其方向与中子反应前的速度方向相同，求：
（1）
H速度多大？
（2）
H和
He运动的轨道半径之比为多少？
（3）当粒子
He旋转了3周时，粒子
H旋转几周？
6 3 |
6 3 |
1 0 |
3 1 |
4 2 |
4 2 |
4 2 |
（1）
3 1 |
（2）
3 1 |
4 2 |
（3）当粒子
4 2 |
3 1 |
分析：（1）核反应中原子核与射线粒子构成的系统动量守恒，则由动量守恒可求得
H速度的大小与方向．
（2）
H和
He在磁场中，做匀速圆周运动，由洛伦兹力提供向心力，得到半径表达式R=
，从而求得R之比．
（3）由周期T=
求得周期之比，再求得粒子
H旋转周数．
3 1 |
（2）
3 1 |
4 2 |
| mv |
| qB |
（3）由周期T=
| 2πm |
| qB |
3 1 |
解答：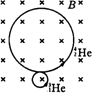
解：（1）36Li核俘获 01n的过程，系统动量守恒，设中子质量为mn，
H的质量为mH，α粒子的质量为mα．
则mnv0=mHv1+mαv2，即v1=
代入数据mn=1u，mα=4 u，mH=3 u，得v1=-1.0×103 m/s，负号表示跟v0的方向相反．
（2）
H和
He在磁场中，运动轨迹如图所示，两个粒子都做匀速圆周运动，由洛伦兹力提供向心力，由qvB=m
，得R=
13H和 24He在磁场中半径之比为 RH：Rα=
：
式中qH=1e，qα=2e，代入解得 RH：Rα=3：40
（2）由周期公式T=
得：
=
=
=
在时间t内旋转的圈数N=
所以它们的转动圈数之比为nH：nα=Tα：TH=2：3
则当α粒子转3周时，粒子
H转动2周．
答：
（1）13H的速度是1.0×103 m/s．
（2）它们的轨道半径之比为3：40．
（3）粒子13H旋转2周．
解：（1）36Li核俘获 01n的过程，系统动量守恒，设中子质量为mn，3 1 |
则mnv0=mHv1+mαv2，即v1=
| mnv0-mαv2 |
| mH |
代入数据mn=1u，mα=4 u，mH=3 u，得v1=-1.0×103 m/s，负号表示跟v0的方向相反．
（2）
3 1 |
4 2 |
| v2 |
| R |
| mv |
| qB |
13H和 24He在磁场中半径之比为 RH：Rα=
| mHv1 |
| qHB |
| mαv2 |
| qαB |
式中qH=1e，qα=2e，代入解得 RH：Rα=3：40
（2）由周期公式T=
| 2πm |
| qB |
| Tα |
| TH |
| qHmα |
| qαmH |
| 1×4 |
| 2×3 |
| 2 |
| 3 |
在时间t内旋转的圈数N=
| t |
| T |
所以它们的转动圈数之比为nH：nα=Tα：TH=2：3
则当α粒子转3周时，粒子
3 1 |
答：
（1）13H的速度是1.0×103 m/s．
（2）它们的轨道半径之比为3：40．
（3）粒子13H旋转2周．
点评：由半径公式分析半径之比的决定物理量，由周期公式分析周期之比的决定物理量，进而求得旋转周数．
练习册系列答案
相关题目
原来静止在匀强磁场中的放射性元素的原子核A，发生衰变后放出的一个射线粒子和反冲核都以垂直于磁感线的方向运动，形成如图所示的8字型轨迹，已知大圆半径是小圆半径的n倍，且绕大圆轨道运动的质点沿顺时针方向旋转．那么：
静止在匀强磁场中的锂核