题目内容
如图所示,A、B是位于水平桌面上的两个质量相等的小木块,离墙壁的距离分别为L和l,与桌面之间的动摩擦因数分别为mA和mB今给A以某一初速度,使之从桌面的右端向左运动,假定A、B之间、B与墙之间的碰撞时间都很短,且碰撞中总动能无损失,若要木块A最后不从桌面上掉下来,则A的初速度最大不能超过________.

答案:见详解
解析:
解析:
mAvA=mAvA′+mBvB′ ① 由于碰撞中总动能无损失,所以
mA=mB=m ③ 联立①②③式解得 vA′=0,vB′=vA,即A与B碰后二者交换速度.所以第一次碰后A停止运动,B滑动;第二次碰后B停止运动,A向右滑动.要求A最后不掉下桌面,它所具有的初动能正好等于A再次回到桌边的全过程中A、B两物体克服摩擦力所做的功,即
所以v0= |

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (2012?杭州模拟)如图所示,A、B两同学用甲、乙两种方式推墙.甲中A向前推B、B向前推墙;乙中A、B同时向前推墙.每人用力的大小都为F,方向水平.已知地面粗糙.则以下说法中正确的是( )
(2012?杭州模拟)如图所示,A、B两同学用甲、乙两种方式推墙.甲中A向前推B、B向前推墙;乙中A、B同时向前推墙.每人用力的大小都为F,方向水平.已知地面粗糙.则以下说法中正确的是( )

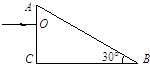


 ,∠B=30°,一束单色光垂直于AC面射向棱镜,入射点为O,试画出光在棱镜中传播的光路图,并求出光射出棱镜时折射角.(不考虑BC面对光线的反射)
,∠B=30°,一束单色光垂直于AC面射向棱镜,入射点为O,试画出光在棱镜中传播的光路图,并求出光射出棱镜时折射角.(不考虑BC面对光线的反射)