题目内容
17. 在反恐演习中,中国特种兵进行了飞行跳伞表演.某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵运动的速度随时间变化的规律如图所示.下列结论正确的是( )
在反恐演习中,中国特种兵进行了飞行跳伞表演.某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵运动的速度随时间变化的规律如图所示.下列结论正确的是( )| A. | 在0~t0时间内加速度不变,在t0~3t0时间内加速度减小 | |
| B. | 降落伞打开后,降落伞和伞兵所受的阻力越来越小 | |
| C. | 在t0~3t0的时间内,平均速度$\overline{v}$>$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| D. | 若第一个伞兵在空中打开降落伞时第二个伞兵立即跳下,则他们在空中的距离先减小后增大 |
分析 速度图象倾斜的直线表示物体做匀加速直线运动,其加速度不变.根据斜率等于加速度,分析t0~3t0时间内加速度如何变化.根据牛顿第二定律分析阻力如何变化.根据“面积”等于位移,将在t0~3t0的时间内物体的位移与匀减速直线运动的位移进行比较,再分析平均速度与$\frac{{v}_{1}+{v}_{2}}{2}$的大小.
解答 解:
A、在0~t0时间伞兵做匀加速直线运动,加速度不变,2t0~3t0时间内图线的斜率逐渐减小,则加速度逐渐减小.故A正确.
B、设降落伞和伞兵的总质量为m,所受的阻力为f,加速度大小为a,根据牛顿第二定律得:f-mg=ma,得f=mg+ma,a逐渐减小,则f也逐渐减小.即降落伞和伞兵所受的阻力越来越小.故B正确.
C、在t0~3t0的时间内,假设伞兵做匀减速直线运动,图象为直线,其平均速度为$\frac{{v}_{1}+{v}_{2}}{2}$,根据“面积”等于位移可知,匀减速直线运动的位移大于伞兵实际运动的位移,则平均速度v<$\frac{{v}_{1}+{v}_{2}}{2}$故C错误;
D、第一个伞兵在空中打开降落伞时的速度比第二个伞兵跳下时速度大,所以两者距离逐渐变大,后来第二个人的速度大于第一个跳伞运动员时,两者距离又减小,故D错误;
故选:AB.
点评 本题根据斜率等于加速度判断加速度的变化.根据“面积”等于位移,分析平均速度的大小.对于匀变速直线运动的平均速度才等于$\frac{{v}_{1}+{v}_{2}}{2}$.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 楞次首先发现电流周围存在磁场 | |
| B. | 法拉第首先发现了电磁感应现象 | |
| C. | 亚里士多德认为力是改变物体运动状态的原因 | |
| D. | 经典力学对宏观物体和微观物体的研究都适用 |
5. 如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )
如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )
 如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )
如图所示,金属线框abcd置于光滑水平桌面上,其右方存在一个有理想边界的方向竖直向下的矩形匀强磁场区,磁场宽度大于线圈宽度.金属线框在水平恒力F作用下向右运动,ab边始终保持与磁场边界平行.ab边进入磁场时线框恰好能做匀速运动.则下列说法中正确的是( )| A. | 线框进入磁场过程,F做的功大于线框内增加的内能 | |
| B. | 线框完全处于磁场中的阶段,F做的功大于线框动能的增加量 | |
| C. | 线框穿出磁场过程中,F做的功等于线框中产生的焦耳热 | |
| D. | 线框穿出磁场过程中,F做的功小于线框中线框中产生的焦耳热 |
12.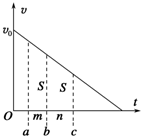 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )
 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )| A. | a=$\frac{2(m+n)S}{(m-n)mn}$ | B. | a=$\frac{2(m-n)S}{(m+n)mn}$ | C. | vb=$\frac{(m+n)S}{mn}$ | D. | vb=$\frac{({m}^{2}+{n}^{2})S}{mn}$ |
2.以下关于光学器件工作原理的叙述中,正确的是( )


| A. | 如图甲中的照相机镜头上涂有一层增透膜,这是利用光的偏振现象,使拍摄橱窗中陈列品等的景象更清晰 | |
| B. | 如图乙是医院手术室中的无影灯,它应用了光的直线传播规律,以避免手术时产生阴影 | |
| C. | 如图丙是医疗检查用的内窥镜,它的核心部件光导纤维之所以能传输光像信号,是利用光的全反射 | |
| D. | 如图丁是自行车的尾灯,平时它本身不发光,但在夜间骑车时,从后面开来的汽车发出的强光照到尾灯后,尾灯自身就会发光而使汽车司机注意到 |
9.对于匀速圆周运动的物体,下列说法中正确的是( )
| A. | 线速度不变 | B. | 角速度不变 | C. | 周期不变 | D. | 向心加速度不变 |
6.下列关于开普勒对于行星运动规律的认识的说法正确的是( )
| A. | 所有行星绕太阳做匀速圆周运动 | |
| B. | 行星与太阳间的连线在相同时间内扫过的角度相等 | |
| C. | 所有行星的轨道的半长轴的二次方跟公转周期的三次方的比值都相同 | |
| D. | 行星轨道半长轴越长,公转周期越大 |
7.地球同步卫星距地面高度为h,地球表面的重力加速度为g,地球半径为R,地球自转的角速度为ω,那么下列表达式表示同步卫星绕地球转动的线速度的是( )
| A. | v=(R+h)ω | B. | v=$\sqrt{\frac{Rg}{R+h}}$ | C. | v=R$\sqrt{\frac{g}{R+h}}$ | D. | v=$\sqrt{gR}$ |
 如图所示,AB为斜面,倾角为30°,小球从A点以初速度v0水平抛出,恰好落到B点.试求:
如图所示,AB为斜面,倾角为30°,小球从A点以初速度v0水平抛出,恰好落到B点.试求: