题目内容
一长为L的绝缘细线下端系质量为m的金属小球，并带有-q的电荷量，在细线的悬点0处放一带电荷量为+q的点电荷．要使金属球能在竖直平面内做完整的圆周运动，求：（1）金属球在最高点受到的库仑力多大？
（2）金属球在最高点的速度至少多大？
（3）如果金属球在最高点的速度为V，则它通过最低点时的速度多大？
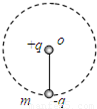
【答案】分析：（1）根据库仑定律求解金属球在最高点受到的库仑力
（2）小球在最高点进行受力分析，当小球在最高点绳子拉力为零时速度最小，根据牛顿第二定律求解．
（3）小球从最高点到最低点的过程中，电场力做功为零，根据动能定理求解．
解答：解：（1）根据库仑定律得金属球在最高点受到的库仑力：F=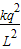
．
（2）当小球在最高点绳子拉力为零时速度最小，最小速度为V1
根据牛顿第二定律得：
mg+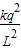
=m
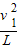
V1=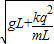
（3）小球从最高点到最低点的过程中，电场力做功为零，如果金属球在最高点的速度为V，设最低点的速度为v2，
据动能定理有：mg?2L=
mv22-
mv2
V2=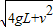
答：（1）金属球在最高点受到的库仑力是
（2）金属球在最高点的速度至少是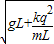
（3）如果金属球在最高点的速度为V，则它通过最低点时的速度是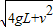
点评：要能正确分析向心力来源，掌握牛顿第二定律和动能定理的应用．
（2）小球在最高点进行受力分析，当小球在最高点绳子拉力为零时速度最小，根据牛顿第二定律求解．
（3）小球从最高点到最低点的过程中，电场力做功为零，根据动能定理求解．
解答：解：（1）根据库仑定律得金属球在最高点受到的库仑力：F=
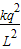．（2）当小球在最高点绳子拉力为零时速度最小，最小速度为V1
根据牛顿第二定律得：
mg+
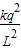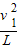
=mV1=
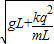
（3）小球从最高点到最低点的过程中，电场力做功为零，如果金属球在最高点的速度为V，设最低点的速度为v2，
据动能定理有：mg?2L=
mv22-mv2V2=
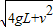
答：（1）金属球在最高点受到的库仑力是
（2）金属球在最高点的速度至少是
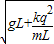
（3）如果金属球在最高点的速度为V，则它通过最低点时的速度是
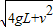
点评：要能正确分析向心力来源，掌握牛顿第二定律和动能定理的应用．
练习册系列答案
备战中考寒假系列答案
相关题目
如图所示，一长为L的绝缘细线下端系一质量为m带电量为q的小球A，细线上端系在水平天花板的O点，在O点正下方固定一带电量为Q的小球B，在库仑力作用下A静止时细线拉力大小为T1，让B的电量变为2Q同时将细线从上端剪掉
如图所示，一长为L的绝缘细线下端拴一质量为m的带电小球，将它置于一匀强电场中，电场强度大小为E，方向水平向右，已知当细线偏离竖直方向的夹角为θ时，小球处于平衡，问：
一长为L的绝缘细线下端系质量为m的金属小球，并带有-q的电荷量，在细线的悬点0处放一带电荷量为+q的点电荷．要使金属球能在竖直平面内做完整的圆周运动，求：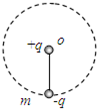
如图所示，一长为L的绝缘细线下端系质量为m的金属小球，并带有-q的电荷量，在细线的悬点o处放一带电荷量为+q的点电荷．要使金属球能在竖直平面内做完整的圆周运动，求：
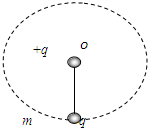如图所示，一长为L的绝缘细线下端系质量为m的金属小球，带-q的电荷量，在细线的悬点O处放一带电荷量为+q的点荷．要使金属球能在竖直平面内做完整的圆周运动．