题目内容
在亚西湾某次护航任务中,为了驱赶索马里海盗,我护航官兵从空中直升机上向海盗船水平发射了一颗警告弹,6s后官兵看到警告弹在海盗船附近爆炸,若爆炸时警告弹的运动方向与水平方向的夹角为30°,空气阻力不计,g=10m/s2,求:(1)直升机发射警告弹时的高度;
(2)警告弹的初速度;
(3)发射警告弹时直升机到海盗船的距离.
【答案】分析:1、警告弹做平抛运动,警告弹的竖直方向上运动的位移就为直升机的高度,警告弹在竖直方向上做自由落体运动,根据自由落体运动的位移公式,可求解直升机的高度.
2、先解出警告弹爆炸瞬间的竖直方向上的速度,再根据速度的夹角公式,可求解处水平速度.
3、根据位移公式解出水平位移,再根据勾股定理计算直升飞机到海盗船的距离.
解答:解:(1)警告弹做平抛运动,警告弹的竖直方向上运动的位移就为直升机的高度.
所以,直升机的高度为h= gt2=
gt2= ×10×62 m=180 m.
×10×62 m=180 m.
(2)警告弹爆炸前瞬间在竖直方向上的速度 vy=g?t=10×6 m/s=60 m/s
因为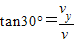
所以v=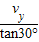 =
=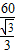 m/s=60
m/s=60 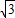 m/s≈104 m/s.
m/s≈104 m/s.
(3)警告弹的水平位移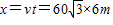
根据勾股定理得
直升机到海盗船的距离 s=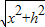 =
=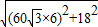 m=
m=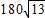 m≈649 m.
m≈649 m.
答:(1)直升机发射警告弹时的高度为180m.
(2)警告弹的初速度为104m/s;
(3)发射警告弹时直升机到海盗船的距离为649m.
点评:此题是平抛运动的常规题,记住并理解平抛运动的规律,画画速度的分解图,有助于理解速度的夹角公式.难度不大,属于中档题.
2、先解出警告弹爆炸瞬间的竖直方向上的速度,再根据速度的夹角公式,可求解处水平速度.
3、根据位移公式解出水平位移,再根据勾股定理计算直升飞机到海盗船的距离.
解答:解:(1)警告弹做平抛运动,警告弹的竖直方向上运动的位移就为直升机的高度.
所以,直升机的高度为h=
 gt2=
gt2= ×10×62 m=180 m.
×10×62 m=180 m.(2)警告弹爆炸前瞬间在竖直方向上的速度 vy=g?t=10×6 m/s=60 m/s
因为
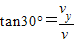
所以v=
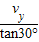 =
=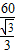 m/s=60
m/s=60 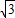 m/s≈104 m/s.
m/s≈104 m/s.(3)警告弹的水平位移
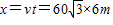
根据勾股定理得
直升机到海盗船的距离 s=
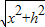 =
=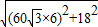 m=
m=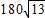 m≈649 m.
m≈649 m.答:(1)直升机发射警告弹时的高度为180m.
(2)警告弹的初速度为104m/s;
(3)发射警告弹时直升机到海盗船的距离为649m.
点评:此题是平抛运动的常规题,记住并理解平抛运动的规律,画画速度的分解图,有助于理解速度的夹角公式.难度不大,属于中档题.

练习册系列答案
相关题目