题目内容
 如图所示,固定斜面的倾角θ=30°,轻弹簧下端固定在斜面底端C点,弹簧处于原长时上端位于B点,空间有平行斜面向下的匀强电场.质量为m,电荷量为+q的小物块,从与B点相距L=0.8m的A点由静止开始下滑,小物块将弹簧压缩到最短后又恰好被弹回到B点.已知物块与斜面间的动摩擦因数为μ=
如图所示,固定斜面的倾角θ=30°,轻弹簧下端固定在斜面底端C点,弹簧处于原长时上端位于B点,空间有平行斜面向下的匀强电场.质量为m,电荷量为+q的小物块,从与B点相距L=0.8m的A点由静止开始下滑,小物块将弹簧压缩到最短后又恰好被弹回到B点.已知物块与斜面间的动摩擦因数为μ=
| ||
| 4 |
| mg |
| 8q |
(1)小物块第一次运动到B点时的速度大小;
(2)弹簧的最大压缩量.
分析:(1)小物块从A到B过程,运用动能定理列式求解即可.
(2)小物块从B点开始将弹簧压缩到最短后又被反弹到B点过程,运用能量守恒求解.
(2)小物块从B点开始将弹簧压缩到最短后又被反弹到B点过程,运用能量守恒求解.
解答:解:(1)小物块从A到B过程中,根据动能定理得:
mgLsin30°+qEL-μmgcos30°L=
mv2… ①
解得B点速度大小为:v=2m/s…②
(2)设弹簧的最大压缩量为x.小物块从B点开始将弹簧压缩到最短后又被反弹到B点过程,由能量守恒定律得:μmgcos30°?2x=
mv2… ③
解得弹簧的最大压缩量为:x=0.27m…④
答:(1)小物块第一次运动到B点时的速度大小是2m/s;
(2)弹簧的最大压缩量是0.27m.
mgLsin30°+qEL-μmgcos30°L=
| 1 |
| 2 |
解得B点速度大小为:v=2m/s…②
(2)设弹簧的最大压缩量为x.小物块从B点开始将弹簧压缩到最短后又被反弹到B点过程,由能量守恒定律得:μmgcos30°?2x=
| 1 |
| 2 |
解得弹簧的最大压缩量为:x=0.27m…④
答:(1)小物块第一次运动到B点时的速度大小是2m/s;
(2)弹簧的最大压缩量是0.27m.
点评:本题涉及到力在空间的积累,运用动能定理研究是常用的思路,而且比较简便.

练习册系列答案
相关题目
 如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( )
如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( ) 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: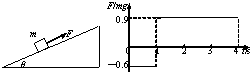 如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为
如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为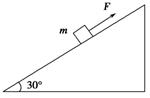
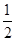 mg B.mg C.
mg B.mg C.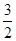 mg D.
mg D.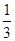 mg
mg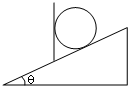 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: