题目内容
4.为验证机械能守恒定律,同学们设计了如图甲所示的装置.装有自动测距仪的木板ABCD水平放置,木板EFGH竖直固定在ABCD上,O1O2为其上的一条竖直线,曲线MN为圆心在O1处半径为L的四分之一圆周的圆弧,自O1M起以10°圆心角为间隔画有刻线.O1处钉有可悬挂细线的小钉,用轻质细线一端连接小球,另一端挂在小钉上,保持球心到O1的距离为L.让细线与竖直方向成θ角由静止释放小球,当细线到达竖直方向时,有强激光束将线熔断.小球落到水平板上时,测距仪自动显示落点到02的距离 现测得O1O2=h,改变θ角释放小球,测得相关数据记录在表一中.
表一
| θ/° | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| s/m | 0.73 | 0.97 | 1.20 | 1.41 | 1.62 | 1.82 | 2.00 |
(1)他导出的理论表达式为s2=s2=4(hL-L2)-4(hL-L2)cosθ;
(2)他将表一数据重新整理,得到表二中的数据,请在坐标纸中画出其图线.
表二:
| θ/° | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| cosθ | 0.87 | 0.77 | 0.64 | 0.50 | 0.34 | 0.17 | 0 |
| s2/m2 | 0.53 | 0.94 | 1.44 | 1.99 | 2.62 | 3.31 | 4.00 |
分析 (1)根据机械能守恒定律求出小球摆到最低点的速度,结合平抛运动的高度求出平抛运动的时间,结合速度和时间求出水平位移,从而得出s2的表达式.
(2)结合表格中的数据描点作图.
解答 解:(1)根据机械能守恒定律有:$mgL(1-cosθ)=\frac{1}{2}m{v}^{2}$,解得v=$\sqrt{2gL(1-cosθ)}$,
根据$h-L=\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2(h-L)}{g}}$,
则水平位移$s=vt=\sqrt{4L(h-L)(1-cosθ)}$.
则s2=4L(h-L)(1-cosθ)=4(hL-L2)-4(hL-L2)cosθ.
(2)根据表格中的数据描点作图,如图所示.
故答案为:(1)s2=4(hL-L2)-4(hL-L2)cosθ,(2)如图所示.
点评 本题考查了平抛运动的规律和机械能守恒得出s2-cosθ的表达式,通过s2-cosθ表达式可知,s2与cosθ成线性关系,所以作出的图线一定是线性图线,不能作成曲线.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
18.下列说法正确的是( )
| A. | 双缝干涉实验中,若把双缝中的一条缝遮住,屏幕上出现一条亮线 | |
| B. | 薄膜干涉条纹产生的原因是同一束光线经薄膜前后两表面反射后相互叠加 | |
| C. | 对于两种介质来说,光在其中传播的速度相对大的介质叫光密介质 | |
| D. | 让自然光通过偏振片P,并以光的传播方向为轴旋转偏振片透射光的强度不变 |
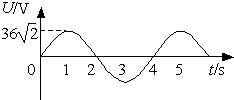
15.矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )

| A. | 1s末线框平面垂直于磁场,通过线框的磁通量变化最快 | |
| B. | 2s末线框平面垂直于磁场,通过线框的磁通量最大 | |
| C. | 交流电压的最大值为36$\sqrt{2}$V,频率为0.50Hz | |
| D. | 交流电压的有效值为36$\sqrt{2}$V,周期为4s |
19.竖直上抛运动的物体,到达最高点时( )
| A. | 物体处于平衡状态 | B. | 具有向上的速度和向上的加速度 | ||
| C. | 速度为零,加速度向上 | D. | 速度为零,加速度向下 |
16.用大小不变的水平拉力作用在物体上,第一次在光滑水平面移动了一段距离,第二次在粗糙水平面移动了相等的距离,下列说法正确的是( )
| A. | 光滑水平面上拉力做功多 | B. | 粗糙水平面上拉力做功多 | ||
| C. | 两次合力做功相同 | D. | 两次拉力做功相同 |
13. 2012年6月16日,刘旺、景海鹏、刘洋三名宇航员搭乘“神舟九号”飞船飞向太空.6月24日执行手动载人交汇对接任务后,于29日10时03分乘返回舱安全返回.返回舱在A点从圆形轨道I进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示.关于返回舱的运动,下列说法中正确的是( )
2012年6月16日,刘旺、景海鹏、刘洋三名宇航员搭乘“神舟九号”飞船飞向太空.6月24日执行手动载人交汇对接任务后,于29日10时03分乘返回舱安全返回.返回舱在A点从圆形轨道I进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示.关于返回舱的运动,下列说法中正确的是( )
 2012年6月16日,刘旺、景海鹏、刘洋三名宇航员搭乘“神舟九号”飞船飞向太空.6月24日执行手动载人交汇对接任务后,于29日10时03分乘返回舱安全返回.返回舱在A点从圆形轨道I进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示.关于返回舱的运动,下列说法中正确的是( )
2012年6月16日,刘旺、景海鹏、刘洋三名宇航员搭乘“神舟九号”飞船飞向太空.6月24日执行手动载人交汇对接任务后,于29日10时03分乘返回舱安全返回.返回舱在A点从圆形轨道I进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示.关于返回舱的运动,下列说法中正确的是( )| A. | 在轨道Ⅱ上经过A的速率大于在轨道I上经过A的速率 | |
| B. | 在轨道Ⅱ上运动的周期大于在轨道I上运动的周期 | |
| C. | 在轨道Ⅱ上经过A的加速度小于在轨道I上经过A的加速度 | |
| D. | 在同一轨道Ⅱ上经过A的速率小于经过B的速率 |
 如图所示,质量为M、半径为r的半圆形凹槽,挨着竖直墙壁放在光滑的水平面上.一质量为m的光滑金属球自凹槽顶端静止滑下.重力加速度为g.求:
如图所示,质量为M、半径为r的半圆形凹槽,挨着竖直墙壁放在光滑的水平面上.一质量为m的光滑金属球自凹槽顶端静止滑下.重力加速度为g.求: 如图所示,在光滑的水平面上停放着一辆平板车C,在车上的左端放有一木块B,车左边紧邻一个固定在竖直平面内、半径为R的$\frac{1}{4}$圆弧形光滑轨道,已知轨道底端的切线水平,且高度与车表面相平.现有另一木块A(木块A、B均可视为质点)从圆弧轨道的顶端由静止释放,然后滑行到车上与B发生碰撞.两木块碰撞后立即粘在一起在平板车上滑行,并与固定在平板车上的水平轻质弹簧作用后被弹回,最后两木块刚好回到车的最左端与车保持相对静止.已知木块A的质量为m,木块B的质量为2m,小车C的质量为3m,重力加速度为g,设木块A、B碰撞的时间极短可以忽略.求:
如图所示,在光滑的水平面上停放着一辆平板车C,在车上的左端放有一木块B,车左边紧邻一个固定在竖直平面内、半径为R的$\frac{1}{4}$圆弧形光滑轨道,已知轨道底端的切线水平,且高度与车表面相平.现有另一木块A(木块A、B均可视为质点)从圆弧轨道的顶端由静止释放,然后滑行到车上与B发生碰撞.两木块碰撞后立即粘在一起在平板车上滑行,并与固定在平板车上的水平轻质弹簧作用后被弹回,最后两木块刚好回到车的最左端与车保持相对静止.已知木块A的质量为m,木块B的质量为2m,小车C的质量为3m,重力加速度为g,设木块A、B碰撞的时间极短可以忽略.求: 如图,长为L=2.0m的水平木板,右端连接一半径为R=1.6m的半圆形柱面,木板的左端有质量均为m=0.1kg的两物块A和B(均视为质点).A和B间有少许塑性炸药.现让两物块一起向右运动,物块与木板间的动摩擦因数均为μ=0.1,当物块运动到木板的最右端瞬时,炸药爆炸,爆炸后B恰好对支持面无压力,A恰好能回到木板左端.g=10m/s2.求:
如图,长为L=2.0m的水平木板,右端连接一半径为R=1.6m的半圆形柱面,木板的左端有质量均为m=0.1kg的两物块A和B(均视为质点).A和B间有少许塑性炸药.现让两物块一起向右运动,物块与木板间的动摩擦因数均为μ=0.1,当物块运动到木板的最右端瞬时,炸药爆炸,爆炸后B恰好对支持面无压力,A恰好能回到木板左端.g=10m/s2.求: