题目内容
 如图所示为一玻璃砖,MN垂直NP,一束单色光从MN上的一点A进入玻璃砖后,又从NP上一点B进入空气中,已知入射角α和出射角β,则
如图所示为一玻璃砖,MN垂直NP,一束单色光从MN上的一点A进入玻璃砖后,又从NP上一点B进入空气中,已知入射角α和出射角β,则①求玻璃的折射率.
②若已知n=
| ||
| 2 |
| π |
| 2 |
分析:①根据光的折射定律,抓住A点折射角和B点入射角之和等于90°,求出玻璃砖的折射率.
②根据求出的折射率的表达式结合数学知识求β的最小值.
②根据求出的折射率的表达式结合数学知识求β的最小值.
解答:解:①设A点的折射角为γ,设B点的折射角为γ',
根据题意可知:γ+γ'=90°
根据折射定律n=
,则sinα=nsinγ
又n=
,则sinβ=nsinγ′
则sin2α+sin2β=n2(sin2γ+sin2γ′)=n2
得:n=
②由前面分析得:n=
两边平方即:
=sin2α+sin2β
可以看出当α取最大值时sin2α最大,则sin2β最小,即β最小,
sin2α最大为1,此时sin2β=
-1=
得:sinβ=
,β=45°
答:①求玻璃的折射率为
.
②若已知n=
,o≤α≤
,β的最小值为45°.
根据题意可知:γ+γ'=90°
根据折射定律n=
| sinα |
| sinγ |
又n=
| sinβ |
| sinγ′ |
则sin2α+sin2β=n2(sin2γ+sin2γ′)=n2
得:n=
| sin2α+sin2β |
②由前面分析得:n=
| sin2α+sin2β |
两边平方即:
| 6 |
| 4 |
可以看出当α取最大值时sin2α最大,则sin2β最小,即β最小,
sin2α最大为1,此时sin2β=
| 6 |
| 4 |
| 1 |
| 2 |
得:sinβ=
| ||
| 2 |
答:①求玻璃的折射率为
| sin2α+sin2β |
②若已知n=
| ||
| 2 |
| π |
| 2 |
点评:解决本题的关键掌握折射定律,根据几何关系进行求解.

练习册系列答案
相关题目
 (2011?朝阳区二模)如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点,且与M点的距离
(2011?朝阳区二模)如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点,且与M点的距离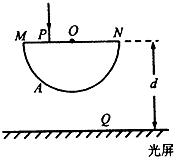 如图所示,一玻璃砖的横截面为半圆形,O为圆心,半径为R,MN为直径,P为OM的中点,MN与水平放置的足够大光屏平行,两者间距为d=
如图所示,一玻璃砖的横截面为半圆形,O为圆心,半径为R,MN为直径,P为OM的中点,MN与水平放置的足够大光屏平行,两者间距为d=
 ,0≤α≤
,0≤α≤ ,求β的最小值.
,求β的最小值.