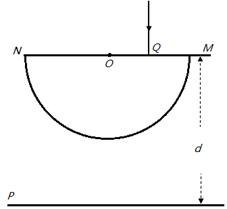
题目内容
 如图所示,一玻璃砖的横截面为半圆形,O为圆心,半径为R,MN为直径,P为OM的中点,MN与水平放置的足够大光屏平行,两者间距为d=
如图所示,一玻璃砖的横截面为半圆形,O为圆心,半径为R,MN为直径,P为OM的中点,MN与水平放置的足够大光屏平行,两者间距为d=| 3 |
| 3 |
分析:光在MN面上是垂直入射,进入圆弧面上时发生折射,作出光路图,求解出各个角度,然后根据折射率公式n=
列式,根据v=
求解玻璃中的速度,最后联立求解.
| sini |
| sinγ |
| c |
| n |
解答: 解:光路图如图所示:
解:光路图如图所示:
设出射点处的入射角为α,折射角为β
由几何关系知:
α=30°
PA=Rcos30°
设光在玻璃转中的传播速度为v,传播时间为t1,则:
v=
PA=vt1
由折射定律得:n=
右图知,AQ=
设光从A到Q所用时间为t2,则:
AQ=ct2
由以上关系可求得从P到Q的时间为:
t=t1+t2=
答:光束从P点到达Q点所用的时间为
.
 解:光路图如图所示:
解:光路图如图所示:设出射点处的入射角为α,折射角为β
由几何关系知:
α=30°
PA=Rcos30°
设光在玻璃转中的传播速度为v,传播时间为t1,则:
v=
| c |
| n |
PA=vt1
由折射定律得:n=
| sinβ |
| sinα |
右图知,AQ=
| d-PA |
| cos(β-α) |
设光从A到Q所用时间为t2,则:
AQ=ct2
由以上关系可求得从P到Q的时间为:
t=t1+t2=
| 5R |
| 2c |
答:光束从P点到达Q点所用的时间为
| 5R |
| 2c |
点评:本题关键画出光路图,然后结合折射率公式n=
和介质中的光速公式v=
列式求解.
| sini |
| sinγ |
| c |
| n |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
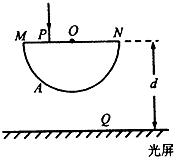
 (2011?朝阳区二模)如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点,且与M点的距离
(2011?朝阳区二模)如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点,且与M点的距离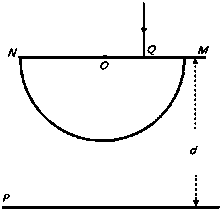 如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点且与M点的距离QM=
如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点且与M点的距离QM=
 R。一单色细光束沿垂直于玻璃砖上表面的方向从P点射入玻璃砖,光从弧形表面上A点射出后到达光屏上Q点。已知玻璃砖对该光的折射率为n=
R。一单色细光束沿垂直于玻璃砖上表面的方向从P点射入玻璃砖,光从弧形表面上A点射出后到达光屏上Q点。已知玻璃砖对该光的折射率为n=
 ,求:
,求: