题目内容
9. 如图所示,三角形金属导轨EOF上放有一根金属杆ab,在外力作用下,保持ab跟OF垂直,以v=5m/s的速度匀速向右移动,设导轨和金属杆都是用粗细相同的同种材料制成的,每米长度的电阻均为r=0.2Ω/m,磁感应强度为B=0.2T,∠EOF=30°,ab与导轨接触良好,ab在O点开始记时,则:
如图所示,三角形金属导轨EOF上放有一根金属杆ab,在外力作用下,保持ab跟OF垂直,以v=5m/s的速度匀速向右移动,设导轨和金属杆都是用粗细相同的同种材料制成的,每米长度的电阻均为r=0.2Ω/m,磁感应强度为B=0.2T,∠EOF=30°,ab与导轨接触良好,ab在O点开始记时,则:(1)3s末电路中的电流为多少?
(2)3s内电路中产生的平均感应电动势为多少?
分析 (1)根据公式E=BLv求感应电动势大小,由已知条件求出总电阻,再根据欧姆定律求电流.
(2)根据法拉第电磁感应定律求平均感应电动势.
解答 解:(1)3s内ab移动的距离 x=vt=5×3m=15m
3s末有效切割长度 L=xtan30°$\frac{BLxtan30°}{(x+xtan30°+\frac{x}{cos30°})r}$
产生的感应电动势为 E=BLv
回路的总电阻 R=(x+L+$\frac{x}{cos30°}$)r
电路中电流为 I=$\frac{E}{R}$=$\frac{BLxtan30°}{(x+xtan30°+\frac{x}{cos30°})r}$=$\frac{Bvtan30°}{(1+tan30°+\frac{1}{cos30°})r}$=$\frac{0.2×5×\frac{\sqrt{3}}{3}}{(1+\frac{\sqrt{3}}{3}+\frac{2}{\sqrt{3}})×0.2}$A=$\frac{5(3-\sqrt{3})}{6}$A
(2)根据法拉第电磁感应定律得
平均感应电动势 $\overline{E}$=$\frac{△Φ}{△t}$=$\frac{B•\frac{1}{2}vt•vttan30°}{△t}$=$\frac{0.2×\frac{1}{2}×{5}^{2}×{3}^{2}×\frac{\sqrt{3}}{3}}{3}$V=$\frac{5\sqrt{3}}{2}$V
答:
(1)3s末电路中的电流为$\frac{5(3-\sqrt{3})}{6}$A.
(2)3s内电路中产生的平均感应电动势为$\frac{5\sqrt{3}}{2}$V.
点评 本题关键要抓住感应电流既与感应电动势有关,还与回路中的电阻有关,根据物理规律推导出电流的解析式,再进行解答.

| A. | 前10s内位移一定是100m | B. | 前10s内位移不一定是100m | ||
| C. | 加速度一定是2m/s2 | D. | 加速度一定是4m/s2 |
| A. | 从螺线管的N极指向S极 | |
| B. | 放在该点的小磁针北极受力的方向 | |
| C. | 放在该点的小磁针的南极受力的方向 | |
| D. | 由于A点在螺线管的内部,所以无法判断 |









 两根相同的匀质棒AB和BC,质量均为m,B点用光滑铰链连接,A端被光滑铰链到一个固定点,棒限于在竖直平面内,A、C原在同一水平线上,∠ABC=90°
两根相同的匀质棒AB和BC,质量均为m,B点用光滑铰链连接,A端被光滑铰链到一个固定点,棒限于在竖直平面内,A、C原在同一水平线上,∠ABC=90°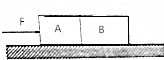 静止在动摩擦因数为μ的水平地面上的两个物体A、B质量分别为m1、和m2,现用一个水平力F推物体A做匀加速运动,求此时A的加速度以及A对B的作用力.
静止在动摩擦因数为μ的水平地面上的两个物体A、B质量分别为m1、和m2,现用一个水平力F推物体A做匀加速运动,求此时A的加速度以及A对B的作用力.