题目内容
18．
如图所示，两轻弹簧a、b悬挂一小铁球处于静止状态，a弹簧与竖直方向成30°角，b弹簧水平，a、b的劲度系数分别为k1和k2，则两弹簧的伸长量x1与x2之比为（ ）| A． | $\frac{k_2}{k_1}$ | B． | $\frac{k_1}{k_2}$ | C． | $\frac{{2{k_2}}}{k_1}$ | D． | $\frac{{2{k_1}}}{k_2}$ |
分析 对小球受力分析，受到重力和两个弹簧的弹力，根据平衡条件并运用合成法得到两个弹力之比，再结合胡克定律求解出伸长量之比．
解答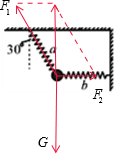 
解：对小球受力分析，受到重力和两个弹簧的弹力，如图
根据平衡条件，有：$\frac{{F}_{2}}{{F}_{1}}$=sin30°=0.5
根据胡克定律，有：
F1=k1x1
F2=k2x2
解得：$\frac{{x}_{1}}{{x}_{2}}=\frac{2{k}_{2}}{{k}_{1}}$
故选：C．
点评 本题考查共点力平衡条件的运用，关键是作图，三力中两个力的合力一定与第三个力等值、反向、共线．
练习册系列答案
相关题目
如图所示，在坐标系xOy的第1、4象限有沿x轴正方向的匀强电场，在第2、3象限内有沿y轴负方向的匀强电场，在第2象限中有垂直于纸面向里的匀强磁场，一质量为m，电荷量为q的带电粒子从y轴上P点沿与y轴正方向45°角的初速度进入第3象限，初速度的大小为v，粒子在第3象限内做匀速直线运动，进入第2象限后粒子做匀速圆周运动，并以与y轴负方向45°角进入第1象限，在第1、4象限里运动后恰好能到达P点，第1、4象限内的电场强度与第2、3象限内的电场强度大小相同，求：
9．北京奥运场馆建设，大量采用对环境有益的新技术，如奥运会场馆周围80%～90%的路灯利用了太阳能发电技术，奥运会90%的洗浴热水采用全玻璃真空太阳能集热技术．太阳能的产生是由于太阳内部高温高压条件下的核反应形成的，其核反应方程是（ ）
| A． | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He | |
| B． | ${\;}_{92}^{238}$U+${\;}_{0}^{1}$n→${\;}_{54}^{136}$Xe+${\;}_{38}^{90}$Sr+10${\;}_{0}^{1}$n | |
| C． | 4${\;}_{1}^{1}$H→${\;}_{2}^{4}$He+2${\;}_{0}^{1}$n | |
| D． | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H |
科研人员乘热气球进行大气环境科学考察，已知气球、座舱、压舱物和科研人员的总质量为1000kg，正常情况下气球能够悬停在空中，但是某次研究中由于气球漏气而逐渐下降，当科研人员发现漏气并及时堵住漏气点时气球下降的速度为1m/s，接下来气球向下做匀加速运动，并且在4s内下降了12m．为使气球安全着陆，科研人员向舱外抛出一定的压舱物（假设抛出压舱物时气球速度不变）．此后发现气球做匀减速运动，下降速度在6s减少3m/s．若空气阻力和泄漏气体的质量均可忽略，下降过程中的重力加速度始终为g=9.5m/s2．则抛出压舱物前，气球的加速度为1m/s2，抛掉的压舱物的质量为150kg．
3．
如图所示，A是一质量为M的盒子，B的质量为$\frac{3M}{4}$，用细绳相连，跨过光滑的定滑轮，A置于倾角为α=30°的斜面上，B悬于斜面之外，处于静止状态．现在向A中缓慢地加入沙子，整个系统始终保持静止，则在加入沙子的过程中（ ）
如图所示，A是一质量为M的盒子，B的质量为$\frac{3M}{4}$，用细绳相连，跨过光滑的定滑轮，A置于倾角为α=30°的斜面上，B悬于斜面之外，处于静止状态．现在向A中缓慢地加入沙子，整个系统始终保持静止，则在加入沙子的过程中（ ）| A． | 绳子拉力大小不变，等于$\frac{3}{4}$Mg | B． | A对斜面的压力逐渐增大 | ||
| C． | A所受的摩擦力先减小后增大 | D． | A所受的摩擦力先增大后减小 |
如图所示，水平放置的传送带以速度v=6m/s向右匀速运行，现将一小煤块轻轻地放在传送带A端，煤块与传送带间的动摩擦因数μ=0.1，若A端与B端相距30m，取g=10m/s2．求：
7．
东方网2014年12月17日消息：据《劳动报》报道，上海海洋大学教授崔维成带队研发的1.1万米载人潜水器最近获得了上海市科委立项支持，这一深度已可抵达目前地球所知 最深的海沟--马里亚纳海沟．这意味着中国载人潜水器将在全世界近100%的海洋范围内自由行动．如图所示为潜水器在某次实验中下潜的速度一时间图象，规定向下为速度的正方向，则（ ）
东方网2014年12月17日消息：据《劳动报》报道，上海海洋大学教授崔维成带队研发的1.1万米载人潜水器最近获得了上海市科委立项支持，这一深度已可抵达目前地球所知 最深的海沟--马里亚纳海沟．这意味着中国载人潜水器将在全世界近100%的海洋范围内自由行动．如图所示为潜水器在某次实验中下潜的速度一时间图象，规定向下为速度的正方向，则（ ）| A． | 3s末潜水器的加速度为零 | |
| B． | 0～1s内潜水器的加速度小于3s-5s内的加速度 | |
| C． | 2s末，潜水器离出发点最远 | |
| D． | 5s末，潜水器回到出发点 |
8．
在如图甲、乙电路中，电阻R、电感线圈L的电阻和灯泡A的电阻均相等．关于灯泡的亮、暗变化情况，下列说法正确的是（ ）
在如图甲、乙电路中，电阻R、电感线圈L的电阻和灯泡A的电阻均相等．关于灯泡的亮、暗变化情况，下列说法正确的是（ ）| A． | 在电路甲中，闭合开关S瞬间，A灯将逐渐变亮 | |
| B． | 在电路乙中，闭合开关S瞬间，A灯将逐渐变亮 | |
| C． | 在电路甲中，断开开关S瞬间，A灯将先变得更亮，然后逐渐变暗 | |
| D． | 在电路乙中，断开开关S瞬间，A灯将立即熄灭 |