题目内容
 如图,倾角为θ的斜面固定不动,斜面上有一个质量为M的盒子A,盒子中有一个刚好与盒内壁相切的质量m的球B,盒内壁光滑而外壁与斜面间的摩擦系数为μ,μ<tgθ,用与斜面平行斜向下的力F推A,讨论球与盒子哪一壁相挤压,这一压力是多少?
如图,倾角为θ的斜面固定不动,斜面上有一个质量为M的盒子A,盒子中有一个刚好与盒内壁相切的质量m的球B,盒内壁光滑而外壁与斜面间的摩擦系数为μ,μ<tgθ,用与斜面平行斜向下的力F推A,讨论球与盒子哪一壁相挤压,这一压力是多少?分析:对整体分析,求出加速度大小,隔离分析求出球与侧壁弹力的大小,然后进行讨论.
解答:解:对整体分析,加速度a=
=
+gsinθ-μgcosθ.
隔离对球分析,N+mgsinθ=ma
N=ma-mgsinθ=
-μmgcosθ.
当N=0时,解得F=μ(M+m)gcosθ,即F=μ(M+m)gcosθ,小球对两壁无压力.
当N>0时,解得F>μ(M+m)gcosθ,即F>μ(M+m)gcosθ,小球对左壁有压力.压力大小为:N=
-μmgcosθ
当N<0时,解得F<μ(M+m)gcosθ,即F<μ(M+m)gcosθ,小球对右壁有压力.压力大小为:N=μmgcosθ-
.
答:F=μ(M+m)gcosθ,小球对两壁无压力.
F>μ(M+m)gcosθ,小球对左壁有压力.压力大小为:N=
-μmgcosθ
F<μ(M+m)gcosθ,小球对右壁有压力.压力大小为:N=μmgcosθ-
.
| F+(M+m)gsinθ-μ(M+m)gcosθ |
| M+m |
| F |
| M+m |
隔离对球分析,N+mgsinθ=ma
N=ma-mgsinθ=
| mF |
| M+m |
当N=0时,解得F=μ(M+m)gcosθ,即F=μ(M+m)gcosθ,小球对两壁无压力.
当N>0时,解得F>μ(M+m)gcosθ,即F>μ(M+m)gcosθ,小球对左壁有压力.压力大小为:N=
| mF |
| M+m |
当N<0时,解得F<μ(M+m)gcosθ,即F<μ(M+m)gcosθ,小球对右壁有压力.压力大小为:N=μmgcosθ-
| mF |
| M+m |
答:F=μ(M+m)gcosθ,小球对两壁无压力.
F>μ(M+m)gcosθ,小球对左壁有压力.压力大小为:N=
| mF |
| M+m |
F<μ(M+m)gcosθ,小球对右壁有压力.压力大小为:N=μmgcosθ-
| mF |
| M+m |
点评:解决本题的关键能够正确地进行受力分析,运用牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
相关题目
 如图,倾角为30°的斜面上放一有支架的小车,支架末端用细线挂一小球.拉着小车沿斜面下滑时,小球与小车相对静止.重力加速度为g,求下述三种情况下小车的加速度.
如图,倾角为30°的斜面上放一有支架的小车,支架末端用细线挂一小球.拉着小车沿斜面下滑时,小球与小车相对静止.重力加速度为g,求下述三种情况下小车的加速度. 如图,倾角为37°的斜面上一重力为50N的木块恰好匀速下滑,sin37°=0.6,求
如图,倾角为37°的斜面上一重力为50N的木块恰好匀速下滑,sin37°=0.6,求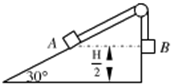 如图,倾角为300的斜面高为H,顶端有一小滑轮,物块A和B的质量分别为m1和m2,通过轻绳连接,不计一切摩擦.开始时两物块都位于离地面高为H/2的位置,由静止释放两物块后,若物块A恰好能到达斜面顶端,求:
如图,倾角为300的斜面高为H,顶端有一小滑轮,物块A和B的质量分别为m1和m2,通过轻绳连接,不计一切摩擦.开始时两物块都位于离地面高为H/2的位置,由静止释放两物块后,若物块A恰好能到达斜面顶端,求: 如图,倾角为15°的斜面上放着一个木箱,100N的拉力F斜向上拉着木箱,F与水平方向成45°角.分别以平行于斜面和垂直于斜面的方向为x轴和y轴建立坐标系,把F分解为沿着两个坐标轴的分力.试在图中作出Fx和Fy,并计算两个分力大小.
如图,倾角为15°的斜面上放着一个木箱,100N的拉力F斜向上拉着木箱,F与水平方向成45°角.分别以平行于斜面和垂直于斜面的方向为x轴和y轴建立坐标系,把F分解为沿着两个坐标轴的分力.试在图中作出Fx和Fy,并计算两个分力大小.