题目内容
如图所示,有一个连通的,上、下两层均与水平面平行的“U”型的光滑金属平行导轨,在导轨面上各放一根完全相同的质量为m的匀质金属杆A1和A2,开始时两根金属杆与轨道垂直,在“U”型导轨的右侧空间存在磁感应强度大小为B、方向竖直向上的匀强磁场,杆A1在磁场中,杆A2在磁场之外.设两导轨面相距为H,平行导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r.现在有同样的金属杆A3从左侧半圆形轨道的中点从静止开始下滑,在下面与金属杆A2发生碰撞,设碰撞后两杆立刻粘在一起并向右运动.求:(1)回路内感应电流的最大值;
(2)在整个运动过程中,感应电流最多产生的热量;
(3)当杆A2、A3与杆A1的速度之比为3:1时,A1受到的安培力大小.

【答案】分析:金属杆A1、A2两杆在同一个金属U形导轨上都做变速运动,运动方向相同(都向右),同一时刻两杆都切割磁感线产生感应电动势,两个感应电动势在空间中的方向相同(都向外),但两个感应电动势在回路中的方向相反,所以总电动势是这两个电动势之差,即E=BL(v1-v2),电流是I= ,方向为金属杆A1中感应电流的方向,因为A1比A2产生的感应电动势大,安培力是F=
,方向为金属杆A1中感应电流的方向,因为A1比A2产生的感应电动势大,安培力是F= ,方向都和速度方向相反(都向左).
,方向都和速度方向相反(都向左).
根据平抛运动规律、动量守恒定律、能量守恒定律解决问题.
解答:解:(1)设A3杆下滑与A2杆碰前速度大小为v,依据动能定理有:
得:
设A3A2碰后速度大小为v1,依据动量守恒有:mv=2mv1
得:
感应电动势的最大值:
闭合回路的总电阻:
电流的最大值:
(2)设A1A2A3杆的共同速度大小为v2,依据动量守恒有:mv=3mv2
得:
依据能量关系,感应电流最多产生的热量:
(3)设A1杆速度大小为v,则A2A3杆的速度大小为3v
依据动量守恒有:mv=mv+2m×3v
得:
此时回路中的感应电动势:
感应电流 A1杆受到的安培力:
A1杆受到的安培力:
答:(1)回路内感应电流的最大值为 ;
;
(2)在整个运动过程中,感应电流最多产生的热量为 mgH;
mgH;
(3)当杆A2、A3与杆A1的速度之比为3:1时,A1受到的安培力大小为 .
.
点评:注重金属杆A1、A2两杆的运动过程分析,清楚同一时刻两杆都切割磁感线产生感应电动势时,根据两个感应电动势在回路中的方向会求出电路中总的感应电动势.
 ,方向为金属杆A1中感应电流的方向,因为A1比A2产生的感应电动势大,安培力是F=
,方向为金属杆A1中感应电流的方向,因为A1比A2产生的感应电动势大,安培力是F= ,方向都和速度方向相反(都向左).
,方向都和速度方向相反(都向左).根据平抛运动规律、动量守恒定律、能量守恒定律解决问题.
解答:解:(1)设A3杆下滑与A2杆碰前速度大小为v,依据动能定理有:

得:

设A3A2碰后速度大小为v1,依据动量守恒有:mv=2mv1
得:

感应电动势的最大值:

闭合回路的总电阻:

电流的最大值:

(2)设A1A2A3杆的共同速度大小为v2,依据动量守恒有:mv=3mv2
得:

依据能量关系,感应电流最多产生的热量:

(3)设A1杆速度大小为v,则A2A3杆的速度大小为3v
依据动量守恒有:mv=mv+2m×3v
得:

此时回路中的感应电动势:

感应电流
 A1杆受到的安培力:
A1杆受到的安培力:
答:(1)回路内感应电流的最大值为
 ;
;(2)在整个运动过程中,感应电流最多产生的热量为
 mgH;
mgH;(3)当杆A2、A3与杆A1的速度之比为3:1时,A1受到的安培力大小为
 .
.点评:注重金属杆A1、A2两杆的运动过程分析,清楚同一时刻两杆都切割磁感线产生感应电动势时,根据两个感应电动势在回路中的方向会求出电路中总的感应电动势.

练习册系列答案
相关题目
 如图所示,有一个连通的,上、下两层均与水平面平行的“U”型的光滑金属平行导轨,在导轨面上各放一根完全相同的质量为m的匀质金属杆A1和A2,开始时两根金属杆与轨道垂直,在“U”型导轨的右侧空间存在磁感应强度大小为B、方向竖直向上的匀强磁场,杆A1在磁场中,杆A2在磁场之外.设两导轨面相距为H,平行导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r.现在有同样的金属杆A3从左侧半圆形轨道的中点从静止开始下滑,在下面与金属杆A2发生碰撞,设碰撞后两杆立刻粘在一起并向右运动.求:
如图所示,有一个连通的,上、下两层均与水平面平行的“U”型的光滑金属平行导轨,在导轨面上各放一根完全相同的质量为m的匀质金属杆A1和A2,开始时两根金属杆与轨道垂直,在“U”型导轨的右侧空间存在磁感应强度大小为B、方向竖直向上的匀强磁场,杆A1在磁场中,杆A2在磁场之外.设两导轨面相距为H,平行导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r.现在有同样的金属杆A3从左侧半圆形轨道的中点从静止开始下滑,在下面与金属杆A2发生碰撞,设碰撞后两杆立刻粘在一起并向右运动.求: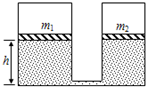 (物理--选修3-3)
(物理--选修3-3)
