题目内容
 用细线吊着一个小球,使小球在水平面内做半径为R匀速圆周运动;圆周运动的水平面距离悬点h,距离水平地面H.若细线突然在A处断裂,则小球经时间t=
用细线吊着一个小球,使小球在水平面内做半径为R匀速圆周运动;圆周运动的水平面距离悬点h,距离水平地面H.若细线突然在A处断裂,则小球经时间t=分析:小球重力和拉力的合力提供圆周运动的向心力,根据牛顿第二定律求出细线断裂时的速度,根据平抛运动的知识求出小球平抛运动的时间和水平位移,结合几何关系求出在地面上的落点P与悬点O在水平面上的投影的O点的距离.
解答:解:设细线与竖直方向上的夹角为θ,小球圆周运动的速度大小为v.
根据牛顿第二定律得:
mgtanθ=m
又 tanθ=
则v=R
.
细线突然在A处断裂后小球开始做平抛运动,则:
由 H=
gt2,得 t=
.
则落点P与A点间的水平距离为 x=vt=R
?
=R
.
根据几何知识得:小球在地面上的落点P与悬点O在水平面上的投影的O点的距离为:S=
=
=R
.
故答案为:
,R
.
根据牛顿第二定律得:
mgtanθ=m
| v2 |
| R |
又 tanθ=
| R |
| h |
则v=R
|
细线突然在A处断裂后小球开始做平抛运动,则:
由 H=
| 1 |
| 2 |
|
则落点P与A点间的水平距离为 x=vt=R
|
|
|
根据几何知识得:小球在地面上的落点P与悬点O在水平面上的投影的O点的距离为:S=
| x2+R2 |
(R
|
|
故答案为:
|
|
点评:本题综合考查了平抛运动和圆周运动,关键掌握平抛运动在水平方向和竖直方向上运动规律以及圆周运动向心力的来源.

练习册系列答案
相关题目
 如图所示,用细线吊着一个小球,使小球在水平面内做匀速圆周运动.关于小球的受力情况,正确的是( )
如图所示,用细线吊着一个小球,使小球在水平面内做匀速圆周运动.关于小球的受力情况,正确的是( )| A、重力 | B、重力、绳子的拉力 | C、重力、绳子的拉力、向心力 | D、重力、向心力 |
 如图所示,用细线吊着一个小球,使小球在水平面内做匀速圆周运动.关于小球的受力情况,正确的是( )
如图所示,用细线吊着一个小球,使小球在水平面内做匀速圆周运动.关于小球的受力情况,正确的是( )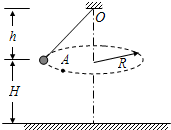 (2007?广州模拟)如图所示,用细线吊着一个小球,使小球在水平面内做半径为R的匀速圆周运动;圆周运动的水平面与悬点的距离为h,与水平地面的距离为H.若细线突在A处断裂,求小球在地面上的落点P与A的水平距离.
(2007?广州模拟)如图所示,用细线吊着一个小球,使小球在水平面内做半径为R的匀速圆周运动;圆周运动的水平面与悬点的距离为h,与水平地面的距离为H.若细线突在A处断裂,求小球在地面上的落点P与A的水平距离.