题目内容
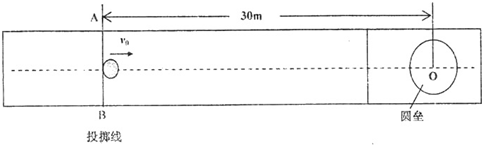
冰壶比赛是在水平冰面上进行的体育项目，比赛场地示意如图所示，比赛时，运动员在投掷线AB 处让冰壶以v=2m/s的初速度向圆垒圆心O点滑出，已知圆垒圆心O到AB线的距离为30m，冰壶与冰面间的动摩擦因数为μ′1=0.008．（g取10m/s2）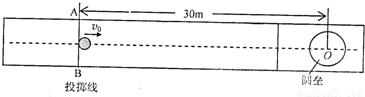
（1）如果在圆垒圆心O有对方的冰壶，为了将对方冰壶撞开，运动员可以用毛刷擦冰壶运行前方的冰面，使冰壶与冰面间的动摩擦力因数减小，若用毛刷擦冰面后动摩擦因数减少至μ2=0.004，则运动员用毛刷擦冰面的长度应大于多少米？
（2）若运动员采用擦刷冰面的方式使冰壶刚好运动到圆垒圆心O点处，那么冰壶运动的最短时间是多少？
【答案】分析：（1）冰壶从投掷线AB滑向圆心O的过程中，滑动摩擦力做功，当冰壶恰好滑到圆心的速度为零时，根据动能定理求出运动员用毛刷擦冰面的最小长度．
（2）根据牛顿第二定律分别求出冰面被刷过和未被刷过的过程冰壶的加速度，由位移公式求出在两个过程上运动的时间，再求解总时间．
解答：解：（1）设滑至O点速度为零，由动能定理得
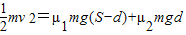
解得d=10m
所以运动员刷冰面的距离应大于10m
（2）由（1）计算可知，在冰面上刷10m时，冰壶到达O处时速度为零．在开始刷冰面10m时，冰壶到达O处运动时间最短
根据牛顿第二定律得
刷过后的加速度为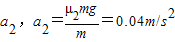
由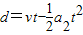
代入解得t=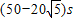
运动d=10m后剩余20m距离以a1做匀减速运动
a1=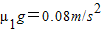
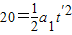
代入解得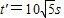
则冰壶运动最短时间为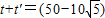
s．
答：（1）运动员用毛刷擦冰面的长度应大于10m；
（2）冰壶运动最短时间为（50-10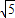
）s．
点评：本题整合了动能定理、牛顿第二定律和运动学公式等多个规律，中等难度，只要细心，可以正确解答．
（2）根据牛顿第二定律分别求出冰面被刷过和未被刷过的过程冰壶的加速度，由位移公式求出在两个过程上运动的时间，再求解总时间．
解答：解：（1）设滑至O点速度为零，由动能定理得
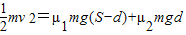
解得d=10m
所以运动员刷冰面的距离应大于10m
（2）由（1）计算可知，在冰面上刷10m时，冰壶到达O处时速度为零．在开始刷冰面10m时，冰壶到达O处运动时间最短
根据牛顿第二定律得
刷过后的加速度为
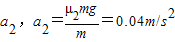
由
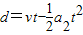
代入解得t=
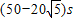
运动d=10m后剩余20m距离以a1做匀减速运动
a1=
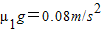
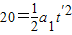
代入解得
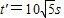
则冰壶运动最短时间为
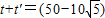s．答：（1）运动员用毛刷擦冰面的长度应大于10m；
（2）冰壶运动最短时间为（50-10
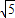）s．点评：本题整合了动能定理、牛顿第二定律和运动学公式等多个规律，中等难度，只要细心，可以正确解答．
练习册系列答案
相关题目
冰壶比赛是在水平冰面上进行的体育项目，由于它的形状像水壶而得名，如图所示．冰壶比赛自1998年被列入冬奥会之后，就成为了越来越普遍的运动项目之一．2010年2月27日在第21届冬奥会上，中国女子冰壶队首次参加冬奥会，获得了铜牌，取得了这个项目的零的突破，令世人瞩目．冰壶比赛的场地如图甲所示．冰道的左端有一个发球区，运动员在发球区边沿的投掷线MN将冰壶以一定的初速度掷出，使冰壶沿着冰道的中心线PO滑行，冰道的右端有一圆形的营垒．以场地上冰壶最终静止时距离营垒圆心O的远近决定胜负．比赛时，为使冰壶滑行得更远，运动员可以用毛刷擦冰壶运行前方的冰面，使冰壶与冰面间的动摩擦因数减小．当对手的冰壶停止在营垒内时，可以用掷出的冰壶与对手的冰壶撞击，使对手的冰壶滑出营垒区．已知冰壶的质量为20kg，营垒的半径为1.8m．设冰壶与冰面间的动摩擦因数μ1=0.008，用毛刷擦冰面后动摩擦因数减小至μ2=0.004．在某次比赛中，若冰壶在发球区受到运动员沿中心线方向推力作用的时间t=10s，使冰壶A在投掷线中点处以v0=2.0m/s的速度沿中心线PO滑出．设冰壶之间的碰撞时间极短，且无机械能损失，不计冰壶自身的大小，g取10m/s2．
