题目内容
3. 如图所示,边长为L的正三角架ABC在竖直平面内,C端用铰链固定在天花板上A、B端各固定一质量为m的小球a、b,AC恰好水平,不计一切摩擦,现释放三角架,则( )
如图所示,边长为L的正三角架ABC在竖直平面内,C端用铰链固定在天花板上A、B端各固定一质量为m的小球a、b,AC恰好水平,不计一切摩擦,现释放三角架,则( )| A. | a、b球最大速度为$\sqrt{\frac{\sqrt{3}}{2}gL}$ | B. | 释放瞬间a球的加速度为g | ||
| C. | a从释放瞬间到最低点一直加速 | D. | b从释放瞬间到最低点一直加速 |
分析 当AB转到水平位置时两球的速度达到最大,根据系统的机械能守恒求出最大速度,并分析两球速度的变化.由牛顿第二定律分析释放瞬间a球的加速度.
解答 解:A、当AB转到水平位置时两球的速度达到最大,此过程中,B的重力势能没有变化.设最大速度为v.
根据系统的机械能守恒得:2×$\frac{1}{2}m{v}^{2}$=mgLsin60°
解得:v=$\sqrt{\frac{\sqrt{3}}{2}gL}$.故A正确.
B、释放瞬间,两球等效重心在AB段的中点.对于两球和整个支架,等效于质量为2m的球位置AB的中点,根据牛顿第二定律得:2mgcos30°=2ma,得 a=$\frac{\sqrt{3}}{2}$.故B错误.
C、a球从释放瞬间到最低点的过程中,两球等效重心先降低后升高,系统的重力势能先减小后增大,由系统的机械能守恒知,动能先增大后减小,则a球的速度先增大后减小,故C错误.
D、b球从释放瞬间到最低点的过程中,两球等效重心一直降低,系统的重力势能一直减小,由系统的机械能守恒知,动能一直增大,则b球的速度一直增大,故D正确.
故选:AD
点评 解决本题的关键是等效法分析整体的重心如何变化,判断重力势能如何变化,从而确定动能的变化情况.

练习册系列答案
相关题目
13.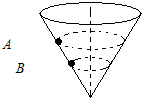 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 线速度vA>vB | B. | 角速度ωA=ωB | C. | 向心力FA=FB | D. | 向心加速度aA<aB |
11. (多选)如图所示,在粗糙水平木板上放一个物块,使木板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )
(多选)如图所示,在粗糙水平木板上放一个物块,使木板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )
 (多选)如图所示,在粗糙水平木板上放一个物块,使木板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )
(多选)如图所示,在粗糙水平木板上放一个物块,使木板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )| A. | 物块始终受到三个力作用 | |
| B. | 物块受到的合外力始终指向圆心 | |
| C. | 在c、d两个位置,物块所受支持力N有最大值,摩擦力f为零 | |
| D. | 在a、b两个位置物块所受摩擦力提供向心力,支持力N=mg |
8. 如图所示,人在河岸上用2m/s的速度匀速拉绳,带动船前进,当绳拉船的部分与水平方向的夹角成60°角时,船的速度大小为( )
如图所示,人在河岸上用2m/s的速度匀速拉绳,带动船前进,当绳拉船的部分与水平方向的夹角成60°角时,船的速度大小为( )
 如图所示,人在河岸上用2m/s的速度匀速拉绳,带动船前进,当绳拉船的部分与水平方向的夹角成60°角时,船的速度大小为( )
如图所示,人在河岸上用2m/s的速度匀速拉绳,带动船前进,当绳拉船的部分与水平方向的夹角成60°角时,船的速度大小为( )| A. | 2$\sqrt{3}$ m/s | B. | 2 m/s | C. | 4 m/s | D. | $\sqrt{3}$m/s |
13. 在体育馆半径为R的半球形穹顶的顶点C正下方P点,以一定初速度v0水平抛出一球,球恰好落在半球面与地面相交的D点,如图所示.设抛球点P到穹顶C的高度为h,不计空气阻力,则( )
在体育馆半径为R的半球形穹顶的顶点C正下方P点,以一定初速度v0水平抛出一球,球恰好落在半球面与地面相交的D点,如图所示.设抛球点P到穹顶C的高度为h,不计空气阻力,则( )
 在体育馆半径为R的半球形穹顶的顶点C正下方P点,以一定初速度v0水平抛出一球,球恰好落在半球面与地面相交的D点,如图所示.设抛球点P到穹顶C的高度为h,不计空气阻力,则( )
在体育馆半径为R的半球形穹顶的顶点C正下方P点,以一定初速度v0水平抛出一球,球恰好落在半球面与地面相交的D点,如图所示.设抛球点P到穹顶C的高度为h,不计空气阻力,则( )| A. | h越大,抛球速度v0越小 | |
| B. | 抛球速度v0有最大值vmax,且vmax=$\sqrt{gR}$ | |
| C. | 抛球速度v0有最小值vmin,且vmin=$\sqrt{\frac{gR}{2}}$ | |
| D. | 抛球速度v0越小,球的位移越小 |

 一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径与细管内径相同的小球(可视为质点).A球的质量为m1,B球的质量为m2.它们沿环形圆管顺时针转动,经过最低点时的速度为v0.设A球运动到最低点时,B球恰运动到最高点,若要此时两球作用于圆管的合力为零,那么B球在最高点的速度多大?
一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径与细管内径相同的小球(可视为质点).A球的质量为m1,B球的质量为m2.它们沿环形圆管顺时针转动,经过最低点时的速度为v0.设A球运动到最低点时,B球恰运动到最高点,若要此时两球作用于圆管的合力为零,那么B球在最高点的速度多大?
 如图所示,边长为a、电阻为R的单匝正方形线圈在磁感应强变大小为B的匀强磁场中,以一条垂直于磁场方向的边OO′为轴匀速转动,转动的角速度为ω,从转轴所在边接出两根导线并串联一阻值也为R的电阻.如图所示,导线的电阻不计,电压表为理想电表.求:
如图所示,边长为a、电阻为R的单匝正方形线圈在磁感应强变大小为B的匀强磁场中,以一条垂直于磁场方向的边OO′为轴匀速转动,转动的角速度为ω,从转轴所在边接出两根导线并串联一阻值也为R的电阻.如图所示,导线的电阻不计,电压表为理想电表.求: