题目内容
8. 三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )
三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )| A. | 运行线速度关系为vA<vB=vC | |
| B. | 运行周期关系为 TA=TB<TC | |
| C. | 向心力大小关系为 FA=FB>FC | |
| D. | 运行半径与周期关系为$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、加速度、周期表达式,根据万有引力定律,可以分析答题.
解答 解:人造卫星绕地球做匀速圆周运动,万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,由图示可知:
rA<rB=rC,
由题意知:MA=MB<MC;
由牛顿第二定律得:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=ma=m(\frac{2π}{T})^{2}r$…①,
A、由①得$v=\sqrt{\frac{GM}{r}}$,所以vA>vB=vC,故A错误;
B、由①得$T=2π\sqrt{\frac{{r}^{3}}{GM}}$,所以TA<TB=TC.故B错误;
C、F=G$\frac{Mm}{{r}^{2}}$,已知rA<rB=rC,MA=MB<MC ,可知FA>FB,FB<FC,故C错误;
D、由①得运行半径与周期关系为$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$,故D正确.
故选:D
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度、周期的表达式,再进行讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )
如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )
 如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )
如图所示接地金属球的半径为R,球外点电荷的电荷量为Q,到金属球的距离为l.该点电荷在金属球上产生的感应电荷的电场在球心的电场强度大小等于( )| A. | $\frac{kQ}{{l}^{2}}$-$\frac{kQ}{{R}^{2}}$ | B. | $\frac{kQ}{{l}^{2}}$+$\frac{kQ}{{R}^{2}}$ | C. | 0 | D. | $\frac{kQ}{(l+R)^{2}}$ |
19.水平传送带在外力作用下始终以速度v匀速运动,某时刻放上一个小物体,初速度大小也是v,方向与传送带的运动方向相反,在滑动摩擦力作用下,最后小物体的速度与传送带的速度相同.在小物体与传送带间有相对运动的过程中,滑动摩擦力对小物体做的功为W,摩擦产生的热量为Q,下列说法中正确的是( )
| A. | W=0,Q=0 | B. | W≠0,Q=0 | C. | W=0,Q≠0 | D. | W≠0,Q≠0 |
16. 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车通过AB线经弯道到达A'B'线,有如图所示的①②③三条路线,其中路线③是以O'为圆心的半圆,OO'=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则下列说法错误的是( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车通过AB线经弯道到达A'B'线,有如图所示的①②③三条路线,其中路线③是以O'为圆心的半圆,OO'=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则下列说法错误的是( )
 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车通过AB线经弯道到达A'B'线,有如图所示的①②③三条路线,其中路线③是以O'为圆心的半圆,OO'=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则下列说法错误的是( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车通过AB线经弯道到达A'B'线,有如图所示的①②③三条路线,其中路线③是以O'为圆心的半圆,OO'=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则下列说法错误的是( )| A. | 选择路线①,赛车经过的路程最短 | |
| B. | 选择路线②,赛车的速率最小 | |
| C. | 选择路线③,赛车所用时间最短 | |
| D. | ①②③三条路线的圆弧上,赛车的向心加速度大小相等 |
3.下列说法正确的是( )
| A. | 最早提出用电场线描述电场的物理学家是富兰克林 | |
| B. | 场强处处为零的区域内,电势一定处处相等 | |
| C. | 电势降落的方向一定是场强方向 | |
| D. | 同一电场中等势面分布越密的地方,电势一定越高 |
17.下列几个关于力学问题的说法中正确的是( )
| A. | 米、千克、牛顿等都是国际单位制中的基本单位 | |
| B. | 摩擦力的方向可能与物体的运动方向垂直 | |
| C. | 放在斜面上的物体,其重力沿垂直斜面的分力就是物体对斜面的压力 | |
| D. | 静止在水平面上的物体所受的重力与水平面给的支持力是一对相互作用力 |
1.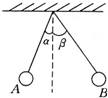 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )| A. | A球的质量较大 | |
| B. | B球的质量较大 | |
| C. | B球受的拉力较大 | |
| D. | 两球接触后,再静止下来,两绝缘细线与竖直方向的夹角变为α′、β′,则有α′=β′ |
 ”,其特点是具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻比较大.
”,其特点是具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻比较大.