题目内容
10. 如图1所示一放在粗糙水平面上的滑块,在一水平向右的外力F作用下运动1s,然后将外力撤走,滑块在摩擦力f的作用下运动3s速度减为零,滑块在这段时间内的速度随时间变化的图象如图2所示.已知整个运动过程中外力F所做的功为W1,克服摩擦力所作的功为W2.则下列关系式正确的是( )
如图1所示一放在粗糙水平面上的滑块,在一水平向右的外力F作用下运动1s,然后将外力撤走,滑块在摩擦力f的作用下运动3s速度减为零,滑块在这段时间内的速度随时间变化的图象如图2所示.已知整个运动过程中外力F所做的功为W1,克服摩擦力所作的功为W2.则下列关系式正确的是( )| A. | F:f=1:3 | B. | F:f=4:1 | C. | W1:W2=1:1 | D. | W1:W2=1:3 |
分析 根据图示图象求出加速度,然后应用牛顿第二定律求出外力与摩擦力的关系,由动能定理求出外力与摩擦力做功的关系.
解答 解:A、由图示图象可知:a1=$\frac{△{v}_{1}}{△{t}_{1}}$=$\frac{{v}_{m}}{1}$=vm,a2=$\frac{△{v}_{2}}{△{t}_{2}}$=$\frac{{v}_{m}}{4-1}$=$\frac{1}{3}$vm,由牛顿第二定律得:a1=$\frac{F-f}{m}$,a2=$\frac{f}{m}$,解得:F:f=4:1,故A错误,B正确;
C、对整个过程,应用动能定理得:W1-W2=0-0,解得:W1=W2,故C正确,D错误;
故选:BC.
点评 本题考查了求做功之比、求力之比,分析清楚滑块的运动过程、根据图示图象求出加速度是解题的关键,应用牛顿第二定律与动能定理可以解题.

练习册系列答案
相关题目
20.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步,下列表述中正确的是( )
| A. | 丹麦天文学家第谷发现了行星运动三定律 | |
| B. | 牛顿发现了万有引力定律测出了引力常量 | |
| C. | 在研究行星运动规律时,开普勒的第三行星运动定律中的k值与地球质量有关 | |
| D. | 1798年英国物理学家卡文迪许通过扭秤实验测量出了万有引力常量 |
18.物体从静止开始做匀加速直线运动,已知第4s内与第2s内的位移之差是12m,则可知( )
| A. | 第1s内的位移为6m | B. | 第2s末的速度为8m/s | ||
| C. | 物体运动的加速度为2m/s2 | D. | 物体在5s内的平均速度为15m/s |
5.我国自行研制的“歼-20”战斗机在某地成功落地滑行,假设该战斗机刚落地滑行时的速度为50m/s,它沿水平面做匀减速直线运动,经过时间60s停下,则停止前滑行的距离为( )
| A. | 1500m | B. | 2000m | C. | 3000m | D. | 不能确定 |
15.关于玻尔的原子模型,下述说法中正确的有( )
| A. | 它提出了完全正确的原子结构模型 | B. | 它发展了汤姆孙的核式结构学说 | ||
| C. | 它引入了普朗克的量子观念 | D. | 它完全抛弃了经典的电磁理论 |
9.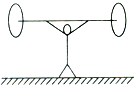 体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
 体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )| A. | 750 N | B. | 800 N | C. | 1000 N | D. | 1200 N |
 如图所示的器材可用来研究电磁感应现象及判定感应电流的方向,其中L1为原线圈,L2为副线圈.
如图所示的器材可用来研究电磁感应现象及判定感应电流的方向,其中L1为原线圈,L2为副线圈.