题目内容
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体接触(未连接),弹簧水平且无形变.用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x,此时物体静止.撤去F后,物体开始向左运动,运动的最大距离为3x.物体与水平面间的动摩擦因数为μ,重力加速度为g.则( )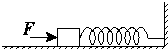
A.撤去F后,物体先做匀加速运动,再做匀减速运动
B.F对弹簧做的功为3μmgx
C.物体做匀减速运动的时间为2
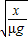
D.物体开始向左运动到速度最大的过程中克服摩擦力做的功为μmgx
【答案】分析:本题通过分析物体的受力情况,来确定其运动情况:撤去F后,物体水平方向上受到弹簧的弹力和滑动摩擦力,滑动摩擦力不变,而弹簧的弹力随着压缩量的减小而减小,可知加速度先减小后增大,物体先做变加速运动,再做变减速运动,最后物体离开弹簧后做匀减速运动;撤去F后,根据牛顿第二定律求解物体刚运动时的加速度大小;物体离开弹簧后通过的最大距离为3x,由牛顿第二定律求得加速度,由运动学位移公式求得时间;当弹簧的弹力与滑动摩擦力大小相等、方向相反时,速度最大,可求得此时弹簧的压缩量,即可求解物体开始向左运动到速度最大的过程中克服摩擦力做的功.
解答:解:A、撤去F后,物体水平方向上受到弹簧的弹力和滑动摩擦力,滑动摩擦力不变,而弹簧的弹力随着压缩量的减小而减小,弹力先大于滑动摩擦力,后小于滑动摩擦力,则物体向左先做加速运动后做减速运动,随着弹力的减小,合外力先减小后增大,则加速度先减小后增大,故物体先做变加速运动,再做变减速运动,最后物体离开弹簧后做匀减速运动;故A错误
B、压缩过程,有功能关系知,外力做功等于弹性势能和克服摩擦力做功;释放后,对物块应用动能定理,弹力做功等于克服摩擦力做功,弹力做功大小等于弹性势能的大小,但两次克服摩擦力做功不同,故F对弹簧做的功大于3μmgx,故B错误
C、弹簧恢复原长后,物体做匀减速运动,加速度大小为a=μg,物体做匀减速运动的时间t=2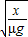 ,故C正确
,故C正确
D、当弹力等于摩擦力时,物体速度增大,此时弹簧没有恢复原长,故D错误
故选C.
点评:本题分析物体的受力情况和运动情况是解答的关键,要抓住加速度与合外力成正比,即可得到加速度是变化的.运用逆向思维研究匀减速运动过程,比较简便
解答:解:A、撤去F后,物体水平方向上受到弹簧的弹力和滑动摩擦力,滑动摩擦力不变,而弹簧的弹力随着压缩量的减小而减小,弹力先大于滑动摩擦力,后小于滑动摩擦力,则物体向左先做加速运动后做减速运动,随着弹力的减小,合外力先减小后增大,则加速度先减小后增大,故物体先做变加速运动,再做变减速运动,最后物体离开弹簧后做匀减速运动;故A错误
B、压缩过程,有功能关系知,外力做功等于弹性势能和克服摩擦力做功;释放后,对物块应用动能定理,弹力做功等于克服摩擦力做功,弹力做功大小等于弹性势能的大小,但两次克服摩擦力做功不同,故F对弹簧做的功大于3μmgx,故B错误
C、弹簧恢复原长后,物体做匀减速运动,加速度大小为a=μg,物体做匀减速运动的时间t=2
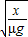 ,故C正确
,故C正确D、当弹力等于摩擦力时,物体速度增大,此时弹簧没有恢复原长,故D错误
故选C.
点评:本题分析物体的受力情况和运动情况是解答的关键,要抓住加速度与合外力成正比,即可得到加速度是变化的.运用逆向思维研究匀减速运动过程,比较简便

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图所示,劲度系数为k的轻弹簧竖直固定在水平面上,上端固定一 质量为m0的托盘,托盘上有一个质量为m的木块.用竖直向下的力将原长为Lo的弹簧压缩后突然撤去外力,则即将脱离m0时的弹簧长度为( )
如图所示,劲度系数为k的轻弹簧竖直固定在水平面上,上端固定一 质量为m0的托盘,托盘上有一个质量为m的木块.用竖直向下的力将原长为Lo的弹簧压缩后突然撤去外力,则即将脱离m0时的弹簧长度为( )| A、Lo | ||
B、
| ||
C、
| ||
D、
|
 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( ) (2013?泰安三模)如图所示,劲度系数为忌的轻弹簧,一端固定在倾角θ=30°的粗糙斜面上,另一端连接一个质量为m的滑块A,滑块与斜面的最大静摩擦力的大小与其滑动摩擦力的大小可视为相等,均为f,且
(2013?泰安三模)如图所示,劲度系数为忌的轻弹簧,一端固定在倾角θ=30°的粗糙斜面上,另一端连接一个质量为m的滑块A,滑块与斜面的最大静摩擦力的大小与其滑动摩擦力的大小可视为相等,均为f,且 如图所示,劲度系数为K的轻质弹簧,一端系在竖直放置的半径为R的圆环顶点P,另一端系一质量为m的小球,小球穿在圆环上作无摩擦的运动.设开始时小球置于A点,弹簧处于自然状态,当小球运动到最底点时速率为υ,对圆环恰好没有压力.下列分析正确的是( )
如图所示,劲度系数为K的轻质弹簧,一端系在竖直放置的半径为R的圆环顶点P,另一端系一质量为m的小球,小球穿在圆环上作无摩擦的运动.设开始时小球置于A点,弹簧处于自然状态,当小球运动到最底点时速率为υ,对圆环恰好没有压力.下列分析正确的是( ) (2011?通州区模拟)如图所示,劲度系数为k1的轻弹簧两端分别与质量为m1、m2的物块1、2拴接,劲度系数为k2的轻弹簧上端与物块2拴接,下端压在桌面上(不拴接),整个系统处于平衡状态.现施力将物块1缓缦地竖直上提,直到下面那个弹簧的下端刚脱离桌面,在此过程中,物块1的重力势能增加了( )
(2011?通州区模拟)如图所示,劲度系数为k1的轻弹簧两端分别与质量为m1、m2的物块1、2拴接,劲度系数为k2的轻弹簧上端与物块2拴接,下端压在桌面上(不拴接),整个系统处于平衡状态.现施力将物块1缓缦地竖直上提,直到下面那个弹簧的下端刚脱离桌面,在此过程中,物块1的重力势能增加了( )