Question

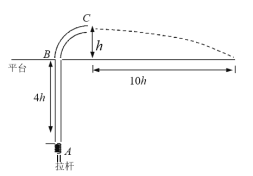
【题目】如图所示为打弹珠的游戏装置，光滑竖直细管 AB 位于平台下方，高度为 4h，直管底部有一竖直轻弹簧，其长度远小于 4h。平台上方 BC 段为一光滑的圆弧管型轨道，其半径为 h，管自身粗细对半径的影响可忽略不计。现拉动拉杆压缩弹簧，再释放拉杆将一质量为 m 的小球弹出，小球弹出后从管口 C 水平飞出，落至平台上，落点距管口C的水平距离为 10h，不计一切阻力，重力加速度为 g，试求：

（1）小球从管口 C 飞出时的速度；

（2）弹簧被压缩后具有的弹性势能；

（3）若平台上方圆弧轨道的半径可调，且保证每次拉动拉杆压缩弹簧的形变量为定值，则当圆弧轨道半径为何值时，小球从管口飞出后距管口 C 的水平距离最大？最大值是多少？

Answer 1

【答案】(1) (2) (3)

【解析】

（1）小球飞出后做平抛运动，竖直方向：

水平方向

10h=v0t

解得

（2）小球从弹出到管口过程，由动能定理：

解得弹簧弹性势能

Ep=30mgh

（3）设1/4圆弧半径为x，由动能定理：

飞出后做平抛运动：

水平距离

s=vt

解得

，

当x=13h时，最大距离为26h。