Question

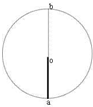
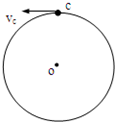
如图所示，质量为m的物体静止在光滑圆轨道的最低点A．现对m施加一大小不变、方向始终沿圆轨道切线方向的力，使物体沿圆周轨道运动

1

4

圆周到达B点，在B点时立即撤去外力F．若要使物体在竖直圆弧轨道内侧能够通过最高点作完整的圆周运动，问所施的外力F至少要多大？

Answer 1

在最高点，根据牛顿第二定律得：mg=m

v2

R

解得：v=

gR

从A到最高点运用动能定理得：
F?

1

4

×2πR-mg?2R=

1

2

mv2-0
解得：F=

5

π

mg
答：所施的外力F至少为

5

π

mg．