题目内容
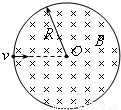
如图所示,半径为R的圆形区域内存在着磁感应强度为B的匀强磁场,方向垂直于纸面向里,一带负电的粒子(不计重力)沿水平方向以速度v正对着磁场圆的圆心入射,通过磁场区域后速度方向偏转了60°角.(1)求粒子的比荷
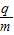 及粒子在磁场中的运动时间;
及粒子在磁场中的运动时间;(2)如果想使粒子通过磁场区域后速度方向的偏转角度最大,在保持入射方向仍然沿水平方向的基础上,需将粒子的入射点向上平移的距离为多少?
【答案】分析:带电粒子沿半径方向射入匀强磁场,做匀速圆周运动,最后将沿半径方向射出磁场.由偏转角可确定圆磁场的半径与轨道半径的关系,从而求出粒子的比荷;由周期公式可求出在磁场中的运动时间.
想使粒子通过磁场区域后速度方向的偏转角度最大,则入射点与出射点的连线过圆磁场的圆心.所以由几何关系可以确定在保持入射方向仍然沿水平方向的基础上,需将粒子的入射点向上平移的距离.
解答:解:
(1)由图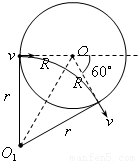 可知
可知
轨迹半径r=Rcot30°①
粒子在洛伦兹力作用下做圆周运动,有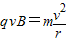 ②
②
由①②两式得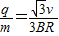 ③
③
运动周期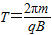 ④
④
在磁场中的运动时间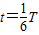 ⑤
⑤
由③④⑤式得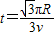 ⑥
⑥
(2)
当粒子的入射点和出射点的连线是磁场圆的直径时,粒子速度偏转的角度最大⑦
由图可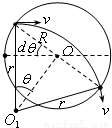 知
知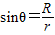 ⑧
⑧
平移距离d=Rsinθ⑨
由①⑧⑨式得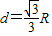 .
.
点评:注意:磁场是圆形,粒子的运动轨迹也是圆形,但不要将这两个半径混淆.同时利用几何关系,可列出已知长度与粒子运动圆弧半径的关系.
带电粒子通过圆磁场偏转最大,则圆弧对应的圆心角最大,即运动一段圆弧的弦必经过圆磁场的圆心.
想使粒子通过磁场区域后速度方向的偏转角度最大,则入射点与出射点的连线过圆磁场的圆心.所以由几何关系可以确定在保持入射方向仍然沿水平方向的基础上,需将粒子的入射点向上平移的距离.
解答:解:
(1)由图
 可知
可知轨迹半径r=Rcot30°①
粒子在洛伦兹力作用下做圆周运动,有
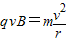 ②
②由①②两式得
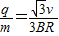 ③
③运动周期
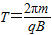 ④
④在磁场中的运动时间
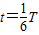 ⑤
⑤由③④⑤式得
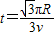 ⑥
⑥(2)
当粒子的入射点和出射点的连线是磁场圆的直径时,粒子速度偏转的角度最大⑦
由图可
 知
知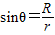 ⑧
⑧平移距离d=Rsinθ⑨
由①⑧⑨式得
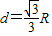 .
.点评:注意:磁场是圆形,粒子的运动轨迹也是圆形,但不要将这两个半径混淆.同时利用几何关系,可列出已知长度与粒子运动圆弧半径的关系.
带电粒子通过圆磁场偏转最大,则圆弧对应的圆心角最大,即运动一段圆弧的弦必经过圆磁场的圆心.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求:
如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求: 如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点.
如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点. 如图所示,半径为R的
如图所示,半径为R的 如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )
如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )