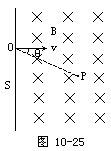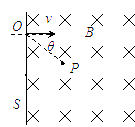题目内容
一个负离子，质量为m，电荷量大小为q，以速率v垂直于屏MN经过小孔O射入存在着匀强磁场的真空室中，如图所示，磁感强度B的方向与离子的运动方向垂直，并垂直于纸面向里．
（1）求离子进入磁场后到达屏MN上时的位置与O点的距离．
（2）如果离子进入磁场后经过时间t到达位置P，试证明：直线OP与离子入射方向之间的夹角θ（弧度）跟t的关系是θ=
t．
（1）求离子进入磁场后到达屏MN上时的位置与O点的距离．
（2）如果离子进入磁场后经过时间t到达位置P，试证明：直线OP与离子入射方向之间的夹角θ（弧度）跟t的关系是θ=
| qB |
| 2m |
（1）由洛伦兹力提供向心力得：
qvB=m
得：r=
入射速度垂直于屏MN射入，由作图几何关系可得出射速度也垂直于屏MN射出，故到达屏MN上时的位置与O点的距离为：
2r=
（2）由几何关系可得，弦切角为圆心角的一半，轨迹所对圆心角为2θ，做圆周运动的周期为：
T=
=
在磁场中运动的时间为：
t=
?
整理得：θ=
答：（1）离子进入磁场后到达屏MN上时的位置与O点的距离为
．
（2）离子进入磁场后经过时间t到达位置P，证得：直线OP与离子入射方向之间的夹角θ（弧度）跟t的关系为θ=
t．
qvB=m
| v2 |
| r |
得：r=
| mv |
| qB |
入射速度垂直于屏MN射入，由作图几何关系可得出射速度也垂直于屏MN射出，故到达屏MN上时的位置与O点的距离为：
2r=
| 2mv |
| qB |
（2）由几何关系可得，弦切角为圆心角的一半，轨迹所对圆心角为2θ，做圆周运动的周期为：
T=
| 2πr |
| v |
| 2πm |
| qB |
在磁场中运动的时间为：
t=
| 2θ |
| 2π |
| 2πm |
| qB |
整理得：θ=
| qBt |
| 2m |
答：（1）离子进入磁场后到达屏MN上时的位置与O点的距离为
| 2mv |
| qB |
（2）离子进入磁场后经过时间t到达位置P，证得：直线OP与离子入射方向之间的夹角θ（弧度）跟t的关系为θ=
| qB |
| 2m |
练习册系列答案
相关题目
一个负离子，质量为m，电量大小为q，垂直于屏S经过小孔O射入存在着匀强磁场的真空室中，如图所示磁场的方向与离子的运动方向垂直，并垂直于纸面向里，其磁感应强度为B．如果离子进入磁场后经过时间t到达位置P，试推导直线OP与离子入射方向之间的夹角θ跟时间t的关系式．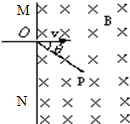
一个负离子，质量为m，电荷量大小为q，以速率v垂直于屏MN经过小孔O射入存在着匀强磁场的真空室中，如图所示，磁感强度B的方向与离子的运动方向垂直，并垂直于纸面向里．
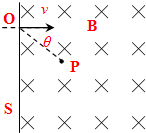（理）一个负离子，质量为m，电量大小为q，以速率v垂直于屏S经过小孔O射入存在着匀强磁场的真空室中，如图所示．磁感应强度B的方向与离子的运动方向垂直，并垂直于图中纸面向里．
？