题目内容
如图所示，在XOY直角坐标系中，OQ与OP分别与X轴正负方向成45，在POQ区域中存在足够大的匀强电场，场强大小为E，其余区域存在匀强磁场，一带电量为+q的质量为m粒子在Y轴上A点（0，-L）以平行于X轴速度v进入第四象项，在QO边界垂直进入电场，后又从PO边界离开电场，不计粒子的重力．求：（1）匀强磁场的磁感应强度大小？
（2）粒子从PO进入磁场的位置坐标？
【答案】分析：（1）粒子在磁场中做匀速圆周运动，由洛伦兹力提供向心力，由几何知识求出轨迹半径，根据牛顿第二定律求出磁感应强度大小；
（2）粒子垂直进入匀速电场后做类平抛运动，沿OQ方向做初速度为零的匀加速运动，OP方向做匀速直线运动，由牛顿第二定律和运动学公式求出粒子射出电场的位置到O点的距离，即可求出粒子从PO进入磁场的位置坐标．
解答：解：（1）设磁感应强度为B，则在磁场中运动，根据牛顿第二定律有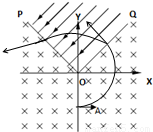
qvB=m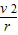
由几何关系可得 r=L
则B=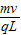
（2）设粒子在电场中运动的加速度大小为α，则根据牛顿第二定律有
a=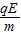
由平抛运动规律知
OQ方向：r=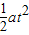
OP方向：S=vt
联立解得，S=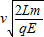
则坐标值为x=-Scos45°=-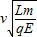
，y=Ssin45°=
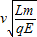，故粒子从PO进入磁场的位置坐标为（-
，
）
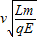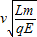答：（1）匀强磁场的磁感应强度大小是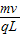
．
（2）粒子从PO进入磁场的位置坐标是（-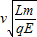
，
）．
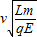点评：本题画出粒子运动轨迹，由几何知识求出轨迹半径是关键；在电场中，运用运动的分解研究类平抛运动．
（2）粒子垂直进入匀速电场后做类平抛运动，沿OQ方向做初速度为零的匀加速运动，OP方向做匀速直线运动，由牛顿第二定律和运动学公式求出粒子射出电场的位置到O点的距离，即可求出粒子从PO进入磁场的位置坐标．
解答：解：（1）设磁感应强度为B，则在磁场中运动，根据牛顿第二定律有
qvB=m
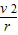
由几何关系可得 r=L
则B=
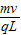
（2）设粒子在电场中运动的加速度大小为α，则根据牛顿第二定律有
a=
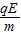
由平抛运动规律知
OQ方向：r=
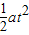
OP方向：S=vt
联立解得，S=
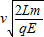
则坐标值为x=-Scos45°=-
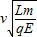，y=Ssin45°=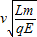，故粒子从PO进入磁场的位置坐标为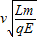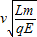（-，）答：（1）匀强磁场的磁感应强度大小是
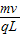．（2）粒子从PO进入磁场的位置坐标是（-
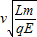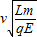，）．点评：本题画出粒子运动轨迹，由几何知识求出轨迹半径是关键；在电场中，运用运动的分解研究类平抛运动．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
如图所示，在竖直平面内有一平面直角坐标系xoy，第一、四象限内存在大小相等方向相反且平行于y轴的匀强电场．在第四象限内某点固定一个点电荷Q（假设该点电荷对第一象限内的电场无影响）．现有一质量为m=9×10-4kg，带电量为 q=3×10-12C的带电微粒从y轴上A 点（y=0.9cm）以初速度v0=0.8m/s垂直y轴射入第一象限经x轴上的B点进入第四象限做匀速圆周运动且轨迹与y轴相切（图中A、B及点电荷Q的位置均未标出）．不考虑以后的运动．（重力加速度g=10m/s2，静电力常量k=9.0×109Nm/C2、，、sin37°=0.6，cos37°=0.8）试求：
如图所示，在竖直平面内建立xOy直角坐标系，Oy表示竖直向上的方向，已知该平面内沿x
如图所示，在竖直的xOy平面上，有一根绝缘光滑的抛物线型硬杆，抛物线方程为y=kx2，其中k为正常数．空间中有沿x轴正向的匀强电场．一个套在杆上带正电的小环在轨道的A点由静止开始滑下，轨道上的B点与A点关于y轴对称．对于带电小环的下列说法，正确的是（ ）
如图所示，在xOy平面内有两根平行y轴水平放置的长直导线，通有沿y轴正方向大小相等的电流I，两导线关于y轴对称，P为x轴上一点，O为z轴上一点，下列说法正确的是（ ）
（2013?成都一模）如图所示，在竖直平面内的直角坐标系xOy的第三象限，同时存在着大小E=1N/C、方向竖直向上的匀强电场和大小 B=