题目内容
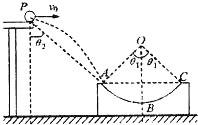 如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一质量为m的小球(可视为质点),从一水平桌面的边缘p点以速度v0向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道,运动到C点速度减小为零.OA、OC与竖直方向的夹角均为θ1 PA与竖直方向的夹角为θ2.下列说法正确的是( )
如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一质量为m的小球(可视为质点),从一水平桌面的边缘p点以速度v0向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道,运动到C点速度减小为零.OA、OC与竖直方向的夹角均为θ1 PA与竖直方向的夹角为θ2.下列说法正确的是( )| A、tanθ1.tanθ2=2 | ||
| B、小球进入A点时重力的瞬时功率为mgv0tanθ1 | ||
C、小球在圆形轨道内摩擦力做的功为
| ||
| D、小球在圆形轨道最低点B处受到轨道的支持力大小为mg |
分析:从图中可以看出,速度与水平方向的夹角为θ1,位移与竖直方向的夹角为θ2.然后求出两个角的正切值.
解答:解:A、平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.速度与水平方向的夹角为θ1,
tanθ1=
=
.位移与竖直方向的夹角为θ2,tanθ2=
=
=
,则tanθ1tanθ2=2.故A正确,
B、小球到达A点的竖直方向的分速度:vy=gt,进入A点时重力的瞬时功率为:PGA=mg?vy=mgv0?tanθ1.故B正确;
C、小球到达A点时,速度与水平方向的夹角为θ1,小球的速度:v=
;
A到C的过程中只有摩擦力做功,得:-W=0-
mv2
所以:W=
mv2=
.故C错误;
D、小球在圆形轨道最低点B处受到轨道的支持力与重力的合力提供小球竖直向上的向心力,所以支持力等于小球的重力.故D错误.
故选:AB.
tanθ1=
| vy |
| v0 |
| gt |
| v0 |
| x |
| y |
| v0t | ||
|
| 2v0 |
| gt |
B、小球到达A点的竖直方向的分速度:vy=gt,进入A点时重力的瞬时功率为:PGA=mg?vy=mgv0?tanθ1.故B正确;
C、小球到达A点时,速度与水平方向的夹角为θ1,小球的速度:v=
| v0 |
| cosθ1 |
A到C的过程中只有摩擦力做功,得:-W=0-
| 1 |
| 2 |
所以:W=
| 1 |
| 2 |
| mv02 |
| 2cos2θ1 |
D、小球在圆形轨道最低点B处受到轨道的支持力与重力的合力提供小球竖直向上的向心力,所以支持力等于小球的重力.故D错误.
故选:AB.
点评:解决本题的关键掌握处理平抛运动的方法,平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.以及知道速度与水平方向夹角的正切值是同一位置位移与水平方向夹角的正切值的两倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一小球从一水平桌面的边缘P点向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道.OA与竖直方向的夹角为θ1,PA与竖直方向的夹角为θ2.下列说法正确的是( )
如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一小球从一水平桌面的边缘P点向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道.OA与竖直方向的夹角为θ1,PA与竖直方向的夹角为θ2.下列说法正确的是( )

