题目内容
如图所示,在光滑绝缘的水平面上固定着两对几何形状完全相同的平行金属板PQ和MN,P、Q与M、N四块金属板相互平行地竖直地放置.已知P、Q之间以及M、N之间的距离都是d=0.2m,极板本身的厚度不计,极板长均为L=0.2m,板间电压都是U=6V且P板电势高.金属板右侧边界以外存在竖直向下的匀强磁场,磁感应强度B=5T,磁场区域足够大.现有一质量m=1×10-4kg,电量q=-2×10-4C的小球在水平面上以初速度v=4m/s从平行板PQ间左侧中点O1沿极板中线O1O1′射入.(1)试求小球刚穿出平行金属板PQ的速度;
(2)若要小球穿出平行金属板PQ后,经磁场偏转射入平行金属板MN中,且在不与极板相碰的前提下,最终从极板MN的左侧中点O2沿中线O2O2′射出,则金属板Q、M间距离是多少?

【答案】分析:(1)小球在PQ金属板间在竖直方向受到的重力和支持力平衡,水平方向只受电场力,初速度平行板PQ,小球做类平抛运动,将小球的运动分解:平行于板的方向做匀速直线运动,垂直于板的方向做匀速直线运动.根据牛顿第二定律和运动学规律求解小球刚穿出平行金属板PQ的速度.
(2)题中P板电势高,在电场中小球向P板偏转,进入后磁场后竖直方向重力和支持力仍平衡,由洛伦兹力提供向心力,小球做匀速圆周运动,根据运动的对称性,画出小球的运动轨迹.在MN板间的运动可看作类平抛运动的逆过程处理.由牛顿定律求出圆周运动的半径,运用几何知识求解金属板Q、M间距离.
解答:解:(1)小球在PQ金属板间做类平抛运动.
小球的加速度a= =60m/s2
=60m/s2
小球在PQ板间运动的时间t= =0.05s
=0.05s
则离开PQ板时的速度为v= =
= =5m/s
=5m/s
设v方向与PQ板中轴线的夹角为θ,则tanθ= =
= ,θ=37°
,θ=37°
(2)作出俯视图如下.
由题,P板电势高,则在电场中小球向P板偏转,进入后磁场后做匀速圆周运动,根据运动的对称性,则必须N板电势高于M板电势,其运动轨迹如图所示.
设小球做匀速圆周运动的半径为R,则
qvB=m ,得R=
,得R= =0.5m
=0.5m
设小球射入和射出磁场时两点间的距离为h,
由几何知识得 h=2Rcosθ=2×0.5×0.8m=0.8m
小球在两平行金属板间偏转的距离y= =7.5×10-3m
=7.5×10-3m
根据对称性可知,金属板Q、M间距离是s=h-2( +y)=0.45m
+y)=0.45m
答:(1)小球刚穿出平行金属板PQ的速度大小为5m/s,方向与板中轴线的夹角为37°;
(2)金属板Q、M间距离是0.45m.
点评:带电粒子在电场和磁场中运动研究方法不同:电场中类平抛运动采用运动的合成和分解,磁场中匀速圆周运动画轨迹.
(2)题中P板电势高,在电场中小球向P板偏转,进入后磁场后竖直方向重力和支持力仍平衡,由洛伦兹力提供向心力,小球做匀速圆周运动,根据运动的对称性,画出小球的运动轨迹.在MN板间的运动可看作类平抛运动的逆过程处理.由牛顿定律求出圆周运动的半径,运用几何知识求解金属板Q、M间距离.
解答:解:(1)小球在PQ金属板间做类平抛运动.
小球的加速度a=
 =60m/s2
=60m/s2小球在PQ板间运动的时间t=
 =0.05s
=0.05s则离开PQ板时的速度为v=
 =
= =5m/s
=5m/s设v方向与PQ板中轴线的夹角为θ,则tanθ=
 =
= ,θ=37°
,θ=37°(2)作出俯视图如下.
由题,P板电势高,则在电场中小球向P板偏转,进入后磁场后做匀速圆周运动,根据运动的对称性,则必须N板电势高于M板电势,其运动轨迹如图所示.

设小球做匀速圆周运动的半径为R,则
qvB=m
 ,得R=
,得R= =0.5m
=0.5m设小球射入和射出磁场时两点间的距离为h,
由几何知识得 h=2Rcosθ=2×0.5×0.8m=0.8m
小球在两平行金属板间偏转的距离y=
 =7.5×10-3m
=7.5×10-3m根据对称性可知,金属板Q、M间距离是s=h-2(
 +y)=0.45m
+y)=0.45m答:(1)小球刚穿出平行金属板PQ的速度大小为5m/s,方向与板中轴线的夹角为37°;
(2)金属板Q、M间距离是0.45m.
点评:带电粒子在电场和磁场中运动研究方法不同:电场中类平抛运动采用运动的合成和分解,磁场中匀速圆周运动画轨迹.

练习册系列答案
相关题目
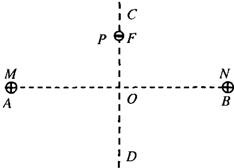 如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )
如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )| A、小球P的带电量缓慢减小,则它往复运动过程中振幅不断减小 | B、小球P的带电量缓慢减小,则它往复运动过程中每次经过O点时的速率不断减小 | C、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中周期不断减小 | D、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中振幅不断减小 |
 如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( )
如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( ) (2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为
(2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为 如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,
如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中, 如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求:
如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求: