题目内容
如图所示，正方形区域EFGH中有垂真于纸面向里的匀强磁场，一个带正电的粒子（不计重力）以一定的速度从EF边的中点M沿既垂直于EF边又垂直于磁场的方向射入磁场，正好从EH边的中点N射出．若该带电粒子的速度减小为原来的一半，其它条件不变，则这个粒子射出磁场的位置是（ ）
A．E点
B．N点
C．H点
D．F点
【答案】分析：带电粒子垂直磁场方向进入磁场后，在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力；根据洛伦兹力提供向心力和轨迹上两点的连线的中垂线都通过圆心找到圆心，确定半径；改变速度后，根据洛伦兹力提供向心力求出新的半径，再次根据洛伦兹力提供向心力找出圆心，画出轨迹．
解答：解：第一次从点M进入磁场，从点N射出，故M、N是轨迹上的两个点，连线的中垂线通过圆心，经过M点时，洛伦兹力提供向心力，判断出洛伦兹力的方向是平行纸面向上并指向C点，故得到C即为圆心，半径R等于线段CM的长度，即正方向边长的一半；
洛伦兹力提供向心力，有
，解得
，该带电粒子的速度减小为原来的一半后，半径减小为一半；
故圆心移到线段CM的中点，轨迹如图；
故选A．
点评：本题关键在于找出圆心、确定轨迹、求出半径，同时要结合洛伦兹力提供向心力进行分析计算．
解答：解：第一次从点M进入磁场，从点N射出，故M、N是轨迹上的两个点，连线的中垂线通过圆心，经过M点时，洛伦兹力提供向心力，判断出洛伦兹力的方向是平行纸面向上并指向C点，故得到C即为圆心，半径R等于线段CM的长度，即正方向边长的一半；
洛伦兹力提供向心力，有
，解得，该带电粒子的速度减小为原来的一半后，半径减小为一半；故圆心移到线段CM的中点，轨迹如图；
故选A．
点评：本题关键在于找出圆心、确定轨迹、求出半径，同时要结合洛伦兹力提供向心力进行分析计算．
练习册系列答案
活力课时同步练习册系列答案
相关题目
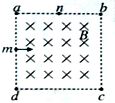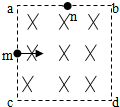如图所示，正方形区域abcd中充满匀强磁场，磁场方向垂直纸面向里，一个氢核从ac边的中点m沿着既垂直于ac边又垂直磁场的方向，以一定速度射入磁场，正好从ab边中点n射出磁场，若将磁场的磁感应强度变为原来的2倍，其他条件不变，则这个氢核射出磁场的位置是
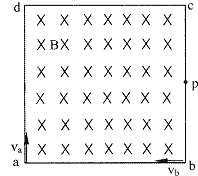如图所示，正方形区域内有垂直于纸面向里的匀强磁场，磁感应强度为B，两个电子分别从a、b两点沿图示方向射人磁场且恰好在bc边的中点p处相遇，不计两电子间的作用力，不计重力，电子的比荷
如图所示，正方形区域MNPQ内有垂直纸面向里的匀强磁场．在外力作用下，一正方形闭合刚性导线框沿QN方向匀速运动，t=0时刻，其四个顶点M′、N′、P′、Q′恰好在磁场边界中点．下列图象中能反映线框所受安培力f的大小随时间t变化规律的是（ ）
如图所示，正方形区域abcd中充满匀强磁场，磁场方向垂直纸面向里．一个氢核从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向，以一定速度射入磁场，正好从ab边中点n射出磁场．现将磁场的磁感应强度变为原来的2倍，其他条件不变，则下列判断正确的是（ ）| A、粒子将从a点射出磁场 | B、粒子将从b射出磁场 | C、粒子在磁场中运动的时间相同 | D、粒子在磁场中运动的时间不同 |