题目内容
10. 在光滑的水平面上,一轻弹簧两端连着A、B两个小物块以v0=8m/s的速度向右运动,弹簧处于原长状态,另有一个小物块C静止在前方,如图所示.已知mA=4kg,mB=mC=2kg,求:
在光滑的水平面上,一轻弹簧两端连着A、B两个小物块以v0=8m/s的速度向右运动,弹簧处于原长状态,另有一个小物块C静止在前方,如图所示.已知mA=4kg,mB=mC=2kg,求:(i)B与C碰撞并粘在一起共同运动时的速度vBC;
(ii)在(i)的情况下,B与C碰撞后弹簧能具有的最大弹性势能.
分析 (i)滑块B与滑块C碰撞过程BC系统的动量守恒,由动量守恒定律求速度vBC;
(2)BC碰撞后压缩弹簧,当系统各部分速度相同时,弹簧压缩量最大,弹性势能最大,由动量守恒定律求出共同速度,由机械能守恒定律求最大弹性势能.
解答 解:(i)B与C碰撞过程与A无关,这一过程动量守恒而机械能不守恒.取向右为正方向,根据动量守恒定律得:
mBv0=(mB+mC)vBC
代入数据解得:vBC=4m/s,水平向右
(ii)在B、C碰撞并粘在一起后,作为一整体与A物块发生持续作用,这一过程动量守恒,机械能也守恒.当弹簧被拉伸到最长或压缩至最短时弹性势能最大,此时整个系统有共同速度,设为v,由动量守恒定律得:
mAv0+(mB+mC)vBC=(mA+mB+mC)v
代入数据解得:v=6m/s
设弹簧的最大弹性势能为Ep,由机械能守恒定律得:
Ep=$\frac{1}{2}$mAv02+$\frac{1}{2}$(mB+mC)vBC2-$\frac{1}{2}$(mA+mB+mC)v2
代入数据解得:Ep=16J.
答:(i)B与C碰撞并粘在一起共同运动时的速度vBC是4m/s,水平向右.
(ii)B与C碰撞后弹簧能具有的最大弹性势能是16J.
点评 本题要理清物体的运动情况,把握临界条件,知道三个物体的速度相同时,弹簧的弹性势能最大,应用动量守恒定律、能量守恒定律即可正确解题.

练习册系列答案
相关题目
1.氢原子的能级公式为En=-$\frac{{E}_{0}}{{n}^{2}}$(n=1,2,3…),式中E0为已知量.氢原子吸收光子从基态跃迁到第二激发态,氢原子增加的质量为( )
| A. | $\frac{2{E}_{0}}{9{c}^{2}}$ | B. | $\frac{4{E}_{0}}{9{c}^{2}}$ | C. | $\frac{5{E}_{0}}{9{c}^{2}}$ | D. | $\frac{8{E}_{0}}{9{c}^{2}}$ |
18.下列叙述正确的是( )
| A. | β衰变所释放的电子是原子核外的电子电离形成的 | |
| B. | 普朗克为了解释黑体辐射现象,第一次提出了能量量子化理论 | |
| C. | 爱因斯坦为了解释光电效应的规律,提出了光子说 | |
| D. | 玻尔将量子观念引入原子领域,其理论能够解释氢原子光谱的特征 | |
| E. | 增大环境的压强或升高温度,都可使放射性物质的半衰期减小 |
5.下列说法正确的是( )
| A. | 气体放出热量,其分子的平均动能可能增大 | |
| B. | 相互间达到热平衡的两物体的内能一定相等 | |
| C. | 气体对容器壁的压强是由气体分子对容器壁的频繁碰撞造成的 | |
| D. | 有些非晶体在一定条件下可以转化为晶体 | |
| E. | 如果气体分子总数不变,而气体温度升高,气体分子的平均动能增大,因此压强必然增大 |
13.小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算如图所示的自行车踏脚板转动的角速度,推算自行车的骑行速度.经过骑行,他已经测到如下的数据:

在时间t内踏脚板转动的圈数为N,那么脚踏板转动的角速度ω=$\frac{2πN}{t}$;要推算自行车的骑行速度,还需要测量的物理量有牙盘的半径r1、飞轮的半径r2、自行车后轮的半径R(填物理量名称及符号);根据测到的物理量写出自行车骑行速度的计算公式为v=$\frac{{R{r_1}ω}}{r_2}$或者$\frac{{2πNR{r_1}}}{{{r_2}t}}$.
| x/m | F/N | v/m•s-1 |
| 0.30 | 1.00 | 0.00 |
| 0.31 | 0.99 | 0.31 |
| 0.32 | 0.95 | 0.44 |
| 0.35 | 0.91 | 0.67 |
| 0.40 | 0.81 | 0.93 |
| 0.45 | 0.74 | 1.10 |
| 0.52 | 0.60 | 1.30 |

在时间t内踏脚板转动的圈数为N,那么脚踏板转动的角速度ω=$\frac{2πN}{t}$;要推算自行车的骑行速度,还需要测量的物理量有牙盘的半径r1、飞轮的半径r2、自行车后轮的半径R(填物理量名称及符号);根据测到的物理量写出自行车骑行速度的计算公式为v=$\frac{{R{r_1}ω}}{r_2}$或者$\frac{{2πNR{r_1}}}{{{r_2}t}}$.
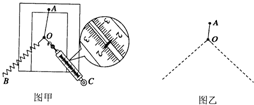 如图甲所示是“探究求共点力合力的方法”
如图甲所示是“探究求共点力合力的方法” (1)在“研究平抛物体的运动”的实验中,为了描出物体的运动轨迹,实验应有下列各个步骤:
(1)在“研究平抛物体的运动”的实验中,为了描出物体的运动轨迹,实验应有下列各个步骤:
 如图为研究碰撞中动量守恒的实验装置,实验时两小球的质量分别为m1和m2,半径为r1和r2,则应满足m1>m2,r1=r2,(填“<”、“=”或“>”),某次实验得出小球的落点情况如图,假设碰撞动量守恒,则碰撞小球质量m1和被碰小球质量m2之比m1:m2=4:1.
如图为研究碰撞中动量守恒的实验装置,实验时两小球的质量分别为m1和m2,半径为r1和r2,则应满足m1>m2,r1=r2,(填“<”、“=”或“>”),某次实验得出小球的落点情况如图,假设碰撞动量守恒,则碰撞小球质量m1和被碰小球质量m2之比m1:m2=4:1.