题目内容
12. 真空中,在半径为r的圆形区域内充满磁感应强度为B的匀强磁场,磁场方向垂直纸面向里,EF是一水平放置的感光板.从圆形磁场最右点A垂直磁场射入大量的质量为m、带电荷量为q、速度为v的粒子,不考虑粒子间的相互作用力及重力,关于这些粒子的运动以下说法正确的是( )
真空中,在半径为r的圆形区域内充满磁感应强度为B的匀强磁场,磁场方向垂直纸面向里,EF是一水平放置的感光板.从圆形磁场最右点A垂直磁场射入大量的质量为m、带电荷量为q、速度为v的粒子,不考虑粒子间的相互作用力及重力,关于这些粒子的运动以下说法正确的是( )| A. | 粒子只要对着圆心入射,出射后均可垂直打在EF上 | |
| B. | 对着圆心入射的粒子,其出射方向的反向延长线不一定过圆心 | |
| C. | 对着圆心入射的粒子,速度越大在磁场中通过的弧长越长,时间也越长 | |
| D. | 只要速度满足v=$\frac{Bqr}{m}$,沿不同方向入射的粒子出射后均可垂直打在EF上 |
分析 带电粒子在圆形磁场中做匀速圆周运动,若入射方向是向着圆心射入,由几何关系知道;带电粒子离开磁场时的速度方向必沿半径方向.若速度大小满足粒子做匀速圆周运动的半径与轨迹圆的半径相等,由几何关系能证明从A点向任意方向入射的粒子从磁场中射出时必垂直向下.
解答  解:三个选项中均涉及到带电粒子和入射方向沿圆心方向,其运动轨迹如图所示,连接两圆心与两交点,由于O′A⊥OA,从B点射出时,作B点的切线,则O′B⊥OB,所以切线方向必通过圆心O,即出射方向必沿半径方向.
解:三个选项中均涉及到带电粒子和入射方向沿圆心方向,其运动轨迹如图所示,连接两圆心与两交点,由于O′A⊥OA,从B点射出时,作B点的切线,则O′B⊥OB,所以切线方向必通过圆心O,即出射方向必沿半径方向.
A、由上述结论,当粒子的速度较大时,由半径公式$r=\frac{mv}{qB}$,则半径较大,偏转角较小,所以粒子有可能打不到屏上,A选项错误.
B、由上述证明,若入射方向与OA成一个夹角时,出射方向必通过圆心,但入射方向是沿着A点切线方向,则带电小球在圆形磁场中做 完整的匀速圆周运动,此种情况出射方向不通过圆心,所以选项B正确.
完整的匀速圆周运动,此种情况出射方向不通过圆心,所以选项B正确.
C、速度越大,半径越大,则偏转角越小,由时间公式t=$\frac{α}{360°}×\frac{2πm}{qB}$,则时间越短,选项C错误.
D、若粒子速度满足v=$\frac{Bqr}{m}$,代入半径公式则带电粒子做圆周运动的半径与磁场区域的半径相等,入射点、出射点及两圆心构成菱形,如图所示,射出磁场时的轨迹半径与最右点的磁场半径平行,即出射粒子的速度方向竖直向下,粒子一定垂直打在MN板上,所以选项D正确.
故选:BD
点评 本题的关键点是D选项,若轨迹圆的半径与磁场圆的半径相等,则从同一点入射速率相等的粒子从磁场中射出时,必垂直于磁场圆与入射点的连线,这是磁聚焦的原理反过来应用.

练习册系列答案
相关题目
9.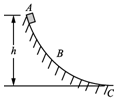 如图所示,ABC是一个位于竖直平面内的圆弧形轨道,高度为h,轨道的末端C处与水平面相切.一个质量为m的小木块从轨道顶端A处由静止释放,到达C处停止,此过程中克服摩擦力做功为W1,到达B处时速度最大为v1,加速度大小为aB;小木块在C处以速度v向左运动,恰好能沿原路回到A处,此过程中克服摩擦力做功为W2,经过B处的速度大小为v2.重力加速度为g.则( )
如图所示,ABC是一个位于竖直平面内的圆弧形轨道,高度为h,轨道的末端C处与水平面相切.一个质量为m的小木块从轨道顶端A处由静止释放,到达C处停止,此过程中克服摩擦力做功为W1,到达B处时速度最大为v1,加速度大小为aB;小木块在C处以速度v向左运动,恰好能沿原路回到A处,此过程中克服摩擦力做功为W2,经过B处的速度大小为v2.重力加速度为g.则( )
 如图所示,ABC是一个位于竖直平面内的圆弧形轨道,高度为h,轨道的末端C处与水平面相切.一个质量为m的小木块从轨道顶端A处由静止释放,到达C处停止,此过程中克服摩擦力做功为W1,到达B处时速度最大为v1,加速度大小为aB;小木块在C处以速度v向左运动,恰好能沿原路回到A处,此过程中克服摩擦力做功为W2,经过B处的速度大小为v2.重力加速度为g.则( )
如图所示,ABC是一个位于竖直平面内的圆弧形轨道,高度为h,轨道的末端C处与水平面相切.一个质量为m的小木块从轨道顶端A处由静止释放,到达C处停止,此过程中克服摩擦力做功为W1,到达B处时速度最大为v1,加速度大小为aB;小木块在C处以速度v向左运动,恰好能沿原路回到A处,此过程中克服摩擦力做功为W2,经过B处的速度大小为v2.重力加速度为g.则( )| A. | v=2$\sqrt{gh}$ | B. | v1<v2 | C. | W1<W2 | D. | aB=0 |
20.有关瞬时速度、平均速度、平均速率,下列说法中正确的是( )
| A. | 平均速度等于瞬时速度的平均值 | |
| B. | 作变速运动的物体,平均速率就是平均速度的大小 | |
| C. | 作变速运动的物体,平均速度是物体通过的路程与所用时间的比值 | |
| D. | 瞬时速度表示物体瞬间运动的快慢 |
7.下列属于离心现象应用的是( )
| A. | 洗衣机甩干衣服 | B. | 田径比赛中的标枪运动 | ||
| C. | 跳水运动员在空中转体 | D. | 体育运动中的铅球运动 |
17. 如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v人,绳某时刻与水平方向夹角为α,则船的运动性质及此时此刻小船速度vx为( )
如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v人,绳某时刻与水平方向夹角为α,则船的运动性质及此时此刻小船速度vx为( )
 如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v人,绳某时刻与水平方向夹角为α,则船的运动性质及此时此刻小船速度vx为( )
如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v人,绳某时刻与水平方向夹角为α,则船的运动性质及此时此刻小船速度vx为( )| A. | 船做匀速直线运动,vx=人cosα | B. | 船做匀速直线运动,vx=$\frac{{v}_{人}}{cosα}$ | ||
| C. | 船做加速运动,vx=v人cosα | D. | 船做加速运动,vx=$\frac{{v}_{人}}{cosα}$ |
4.提出日心说的科学家是以下哪位( )
| A. | 哥白尼 | B. | 开普勒 | C. | 托勒密 | D. | 伽利略 |
2. 质量分别为2m和m的A、B 两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )
质量分别为2m和m的A、B 两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )
 质量分别为2m和m的A、B 两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )
质量分别为2m和m的A、B 两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )| A. | F1和F2大小相等 | |
| B. | F1和F2对A、B做功之比为2:1 | |
| C. | A、B所受摩擦力大小相等 | |
| D. | 全过程中摩擦力对A、B做功之比为1:1 |
 如图OAB一个阻值为R的导线折成一个圆心角为直角的扇形,t=0时OB边和匀强磁场的上边缘重合,磁场垂直纸面向外,现使导线框绕过O点的垂直于导线平面的轴以角速度ω顺时针匀速转动,若以O→B→A方向为电流正方向,则从t=0开始转动一周的过程中,电流随ωt变化的图象是( )
如图OAB一个阻值为R的导线折成一个圆心角为直角的扇形,t=0时OB边和匀强磁场的上边缘重合,磁场垂直纸面向外,现使导线框绕过O点的垂直于导线平面的轴以角速度ω顺时针匀速转动,若以O→B→A方向为电流正方向,则从t=0开始转动一周的过程中,电流随ωt变化的图象是( )



