Question

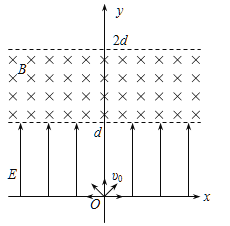
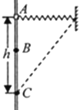
【题目】如图所示，在倾角为30°的光滑斜面上放置一质量为m的物块B，B的下端连接一轻质弹簧，弹簧下端与挡板相连接，B平衡时，弹簧的压缩量为x0，O点为弹簧的原长位置。在斜面顶端另有一质量也为m的物块A，距物块B为3x0，现让A从静止开始沿斜面下滑，A与B相碰后立即一起沿斜面向下运动，但不粘连，它们到达最低点后又一起向上运动，并恰好回到O点(A、B均视为质点)。试求：

(1)A、B相碰后瞬间的共同速度的大小；

(2)A、B相碰前弹簧具有的弹性势能；

(3)若在斜面顶端再连接一光滑的半径R＝x0的半圆轨道PQ，圆弧轨道与斜面相切于最高点P，现让物块A以初速度v从P点沿斜面下滑，与B碰后返回到P点还具有向上的速度，则v为多大时物块A恰能通过圆弧轨道的最高点？

Answer 1

【答案】(1) (2) (3)

【解析】

(1)A与B碰撞前后，设A的速度分别是和

A下滑过程中，机械能守恒，有：

解得： ①

又因A与B碰撞过程中，动量守恒，有：

②

联立①②得

(2)碰后，A、B和弹簧组成的系统在运动过程中，机械能守恒。

则有：

又由（1）得

代入解得：

③

(3)设物块A在最高点C的速度是

物块A恰能通过圆弧轨道的最高点C点时，重力提供向心力，得：

C点相对于O点的高度，如图所示：

物块从O到C的过程中机械能守恒，得：

设A与B碰撞后共同的速度为，碰撞前A的速度为，

物块A从P到与B碰撞前的过程中机械能守恒，得：

A与B碰撞的过程中动量守恒，得：

A与B碰撞结束后到O的过程中机械能守恒，得：

⑩

由于A与B不粘连，到达O点时，滑块B开始受到弹簧的拉力，A与B分离。

综合上述式子解得：