题目内容
如图所示有一根玻璃管，内径为d，外径为2d，折射率为n=| 3 |
分析：当光线从玻璃管内射到玻璃管的外壁时，若入射角大于临界角，会发生全反射，将不能从玻璃管的外壁射出玻璃管，根据临界角公式sinC=
，求出临界角的范围，由折射定律求出折射角，运用几何知识和产生全反射的条件进行判断．并求出各处射出的光线与A点入射光线的夹角．
| 1 |
| n |
解答：解：设光从玻璃到空气临界角为C，sinC=
=
得30°＜C＜45°；
设光进入玻璃管时折射角为θ，射向内表面的入射角为β．
据折射定律有：sinα=nsinθ，得θ=30°；
此时光线刚好与玻璃内表面相切，光照射到外表面时的入射角β为30°，因30°＜C＜45°，可知入射角β小于C，则有光射出玻璃管．
由光路可逆分析，折射光线对应的折射角为60°，此时射出的光线2与A点入射光线1的夹角为60°；在此位置有部分光线发生反射，再在另一位置出射，其入射角为30°，对应的折射角为60°，此时射出的光线3与A点入射光线1的夹角为180°；还有部分光线进一步发生反射在A点处出射，此时射出的光线4与A点入射光线1的夹角为60°．
故有光线射出的位置有三处，各处射出的光线与A点入射光线的夹角分别为：第一处60°（或120°）；第二处180°；第三处60°（或120°）．
答：有光线从玻璃管的外壁射出玻璃管，且有光线射出的位置有三处，各处射出的光线与A点入射光线的夹角分别为：第一处60°（或120°）；第二处180°；第三处60°（或120°）．
| 1 |
| n |
| 1 | ||
|
得30°＜C＜45°；
设光进入玻璃管时折射角为θ，射向内表面的入射角为β．
据折射定律有：sinα=nsinθ，得θ=30°；
此时光线刚好与玻璃内表面相切，光照射到外表面时的入射角β为30°，因30°＜C＜45°，可知入射角β小于C，则有光射出玻璃管．
由光路可逆分析，折射光线对应的折射角为60°，此时射出的光线2与A点入射光线1的夹角为60°；在此位置有部分光线发生反射，再在另一位置出射，其入射角为30°，对应的折射角为60°，此时射出的光线3与A点入射光线1的夹角为180°；还有部分光线进一步发生反射在A点处出射，此时射出的光线4与A点入射光线1的夹角为60°．
故有光线射出的位置有三处，各处射出的光线与A点入射光线的夹角分别为：第一处60°（或120°）；第二处180°；第三处60°（或120°）．
答：有光线从玻璃管的外壁射出玻璃管，且有光线射出的位置有三处，各处射出的光线与A点入射光线的夹角分别为：第一处60°（或120°）；第二处180°；第三处60°（或120°）．
点评：本题考查了光的折射、全反射的知识，能正确利用几何知识是解决此类问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一根粗细均匀的玻璃管长为80cm，一端开口，一端封闭；管内有一段25cm长的水银柱将一段空气柱封闭于管中，当玻璃管水平放置时，空气柱长为40cm，问当玻璃管开口的向下竖直放置时，管内空气柱长为多少？（假设温度保持不变，外界大气压为75cmHg）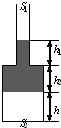
如图所示，一根上细下粗、粗端与细端都粗细均匀的玻璃管上端开口、下端封闭，横截面积S2=4S1．上端与大气连通，管中有一段水银封闭了一定质量的理想气体，空气柱长度为h，水银柱高度h1=h2=h．已知大气压强为po，水银密度为ρ，重力加速度为g，初始温度为To．求：
，图乙是它的截面．有一束光线从玻璃管的外侧面上的A点垂直于玻璃管中心轴线射入．若入射角α为60°，则有无光线从玻璃管的外壁射出玻璃管？如果有，则有光线射出的位置有几处，并求出各处射出的光线与A点入射光线的夹角是多大？如果没有，请说明理由．需作出光路图．
，图乙是它的截面．有一束光线从玻璃管的外侧面上的A点垂直于玻璃管中心轴线射入．若入射角α为60°，则有无光线从玻璃管的外壁射出玻璃管？如果有，则有光线射出的位置有几处，并求出各处射出的光线与A点入射光线的夹角是多大？如果没有，请说明理由．需作出光路图。