题目内容
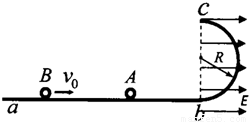
如图,abc是光滑的轨道,其中ab是水平的,bc是位于竖直平面内与ab相切的半圆轨道,半径为R.bc线的右侧空间存在方向水平向右的匀强电场,场强为E;bc线的左侧(不含bc线)空间存在垂直轨道平面的匀强磁场.带电量为+q目的小球A的质量为m.静止在水平轨道上.另一质量为2m的不带电小球Bv0=
的初速度与小球A发生正碰.已知碰后小球A恰好能通过半圆的最高点C,随后进入磁场后作匀速直线运动.已知碰撞及运动中A球的电量保持不变,g为重力加速度.求:
(1)匀强磁场的磁感应强度B的大小和方向;
(2)碰撞结束后A、B两球的速率vA和vB;
(3)分析说明两球发生的是否弹性碰撞.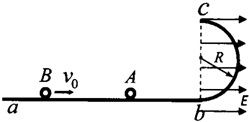
| 5gR |
(1)匀强磁场的磁感应强度B的大小和方向;
(2)碰撞结束后A、B两球的速率vA和vB;
(3)分析说明两球发生的是否弹性碰撞.

(1)设碰后小球A在半圆的最高点c时的速度为v,小球A恰好刚能通过c点,则对小球A在竖直方向上有:
mg=mv2/R----------------------①
在磁场中匀速运动,也就是处于受力平衡状态,有:
qvB=mg--------------------------②
联立解得:B=
--------------------③
由左手定则可以判断,磁场方向应该垂直纸面向外
(2)对小球A从碰后到半圆的最高点c的过程,由动能定理得:
-mg?2R=
mv2/2-
mvA2/2----------------------④
对碰撞的过程,由动量守恒定律得:
2mv0=2mvB+mvA-------------------------------⑤
联立①④⑤各式并代入数据解得:
vA=
vB=
(3)碰撞中系统机械能(或动能)的损失为:
△E=
?2mv02-(
mvA2+
mvB2)=
mgR>0
说明碰撞中系统机械能(或动能)减小,因此两球发生的是非弹性碰撞.
故答案为:(1)匀强磁场的磁感应强度B的大小为
,方向垂直纸面向外;
(2)碰撞结束后A的速率为
,B的速率为
;
(3)两球发生的是非弹性碰撞.
mg=mv2/R----------------------①
在磁场中匀速运动,也就是处于受力平衡状态,有:
qvB=mg--------------------------②
联立解得:B=
| m |
| q |
|
由左手定则可以判断,磁场方向应该垂直纸面向外
(2)对小球A从碰后到半圆的最高点c的过程,由动能定理得:
-mg?2R=
| 1 |
| 2 |
| 1 |
| 2 |
对碰撞的过程,由动量守恒定律得:
2mv0=2mvB+mvA-------------------------------⑤
联立①④⑤各式并代入数据解得:
vA=
| 5gR |
vB=
| ||
| 2 |
(3)碰撞中系统机械能(或动能)的损失为:
△E=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
说明碰撞中系统机械能(或动能)减小,因此两球发生的是非弹性碰撞.
故答案为:(1)匀强磁场的磁感应强度B的大小为
| m |
| q |
|
(2)碰撞结束后A的速率为
| 5gR |
| ||
| 2 |
(3)两球发生的是非弹性碰撞.

练习册系列答案
相关题目
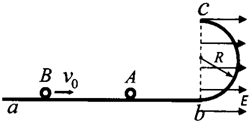 如图,abc是光滑的轨道,其中ab是水平的,bc是位于竖直平面内与ab相切的半圆轨道,半径为R.bc线的右侧空间存在方向水平向右的匀强电场,场强为E;bc线的左侧(不含bc线)空间存在垂直轨道平面的匀强磁场.带电量为+q目的小球A的质量为m.静止在水平轨道上.另一质量为2m的不带电小球B
如图,abc是光滑的轨道,其中ab是水平的,bc是位于竖直平面内与ab相切的半圆轨道,半径为R.bc线的右侧空间存在方向水平向右的匀强电场,场强为E;bc线的左侧(不含bc线)空间存在垂直轨道平面的匀强磁场.带电量为+q目的小球A的质量为m.静止在水平轨道上.另一质量为2m的不带电小球B
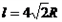 处,重力加速度g=10m/s
处,重力加速度g=10m/s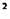 ,求:
,求: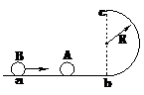
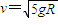 的初速度与小球A发生正碰.已知碰后小球A恰好能通过半圆的最高点C,随后进入磁场后作匀速直线运动.已知碰撞及运动中A球的电量保持不变,g为重力加速度.求:
的初速度与小球A发生正碰.已知碰后小球A恰好能通过半圆的最高点C,随后进入磁场后作匀速直线运动.已知碰撞及运动中A球的电量保持不变,g为重力加速度.求: