题目内容
15. 在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求小球做圆周运动的周期、角速度、线速度.
在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求小球做圆周运动的周期、角速度、线速度.
分析 对小球受力分析,小球受重力,绳的拉力,合力水平方向指向圆心,根据几何关系求解小球所受合力,再根据合力提供圆周运动向心力求得小球圆周运动的周期、角速度和线速度.
解答 解:如图对小球进行受力分析,受重力和绳子的拉力, 根据力的合成可知:F合=mgtanθ
根据力的合成可知:F合=mgtanθ
由图可知,小球圆周运动的半径为:r=Lsinθ
小球所受合力提供小球圆周运动的向心力有:
${F}_{合}=mgtanθ=mr\frac{4{π}^{2}}{{T}^{2}}=mr{ω}^{2}=m\frac{{v}^{2}}{r}$
可得小球圆周运动的周期为:T=$T=\sqrt{\frac{4{π}^{2}r}{gtanθ}}=2π\sqrt{\frac{Lsinθ}{gtanθ}}$=$2π\sqrt{\frac{Lcosθ}{g}}$
小球的运动的角速度为:$ω=\frac{2π}{T}=\frac{2π}{2π\sqrt{\frac{Lcosθ}{g}}}$=$\sqrt{\frac{g}{Lcosθ}}$
小球运动的线速度为:$v=\sqrt{grtanθ}$=$\sqrt{gLsinθtanθ}$
答:小球做圆周运动的周期为$2π\sqrt{\frac{Lcosθ}{g}}$,角速度为$\sqrt{\frac{g}{Lcosθ}}$,线速度为$\sqrt{gLsinθtanθ}$.
点评 解决本题的关键是知道小球在水平面内圆周运动的向心力由绳的拉力和重力的合力提供,正确的受力分析是正确解题的基础.

练习册系列答案
相关题目
3.设地球表面的重力加速度为g0,物体在距地心4R(R为地球半径)处,由于地球的作用而产生的重力加速度为g,则g:g0为( )
| A. | 16:1 | B. | 4:1 | C. | 1:4 | D. | 1:16 |
20.关于行星绕太阳运动,下列说法正确的是( )
| A. | 行星在椭圆轨道上绕太阳运动的过程中,其速度与行星和太阳之间的距离有关,距离小时速度小,距离大时速度大 | |
| B. | 行星在椭圆轨道上绕太阳运动,太阳在椭圆轨道的一个焦点上 | |
| C. | 所有行星绕太阳运动的周期都是相等的 | |
| D. | 行星在椭圆轨道上绕太阳运动的过程中,太阳对行星的引力是不变的 |
7. 如图所示,用跟水平方向成α角的推力F推重量为G的木块沿天花板向右运动,木块和天花板间的动摩擦因数为μ,则木块所受的摩擦力大小一定是( )
如图所示,用跟水平方向成α角的推力F推重量为G的木块沿天花板向右运动,木块和天花板间的动摩擦因数为μ,则木块所受的摩擦力大小一定是( )
 如图所示,用跟水平方向成α角的推力F推重量为G的木块沿天花板向右运动,木块和天花板间的动摩擦因数为μ,则木块所受的摩擦力大小一定是( )
如图所示,用跟水平方向成α角的推力F推重量为G的木块沿天花板向右运动,木块和天花板间的动摩擦因数为μ,则木块所受的摩擦力大小一定是( )| A. | F•cosα | B. | μ(mg+Fsinα) | C. | μ(Fsinα-mg) | D. | 无法确定 |
4.下列关于点电荷的说法中,正确的是( )
| A. | 体积大的带电体一定不是点电荷 | |
| B. | 当两个带电体的形状对它们相互作用力的影响可忽略时,这两个带电体可看做点电荷 | |
| C. | 点电荷就是体积足够小的电荷 | |
| D. | 点电荷是电荷量和体积都很小的带电体 |
 如图所示,AB为一斜面,小球从A处以一定初速度v0水平抛出,落地点恰在B点,已知θ=37°,斜面长为LAB=75m,求:
如图所示,AB为一斜面,小球从A处以一定初速度v0水平抛出,落地点恰在B点,已知θ=37°,斜面长为LAB=75m,求: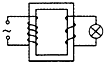



 如图所示G为指针在中央的灵敏电流表,连接在直流电路中时的偏转情况.今把它与一线圈串联进行电磁感应实验,则(2)中电流计的指针从中央向右偏转;图(3)中的条形磁铁上端为N极.
如图所示G为指针在中央的灵敏电流表,连接在直流电路中时的偏转情况.今把它与一线圈串联进行电磁感应实验,则(2)中电流计的指针从中央向右偏转;图(3)中的条形磁铁上端为N极. 微耕机俗称“铁牛”,以小型柴油机或汽油机为动力,具有重量轻,体积小等特点,广泛适用于平原、山区、丘陵的旱地、水田、果园等.如图1所示为一款可遥控的履带式柴油微耕机,其质量为100kg,额定功率4kW.现遥控该微耕机以额定功率匀速从A处经倾角α=30°,长L=100m的斜坡行驶到B处犁地,斜坡对它的阻力恒为1500N(如图2).求:
微耕机俗称“铁牛”,以小型柴油机或汽油机为动力,具有重量轻,体积小等特点,广泛适用于平原、山区、丘陵的旱地、水田、果园等.如图1所示为一款可遥控的履带式柴油微耕机,其质量为100kg,额定功率4kW.现遥控该微耕机以额定功率匀速从A处经倾角α=30°,长L=100m的斜坡行驶到B处犁地,斜坡对它的阻力恒为1500N(如图2).求: