题目内容
13. 如图所示,在边界上方存在着范围足够大垂直纸面向里的匀强磁场,有两个电荷量、质量均相同的正、负粒子(不计重力),从边界上O点以相同的速度先后射入磁场中,入射方向与边界成θ角,则正、负粒子在磁场中( )
如图所示,在边界上方存在着范围足够大垂直纸面向里的匀强磁场,有两个电荷量、质量均相同的正、负粒子(不计重力),从边界上O点以相同的速度先后射入磁场中,入射方向与边界成θ角,则正、负粒子在磁场中( )| A. | 运动轨迹的半径相同 | |
| B. | 返回边界所用的时间相同 | |
| C. | 返回边界时速度大小相等,方向不同 | |
| D. | 返回边界时与O点的距离相等 |
分析 由题正负离子的质量与电量相同,进入同一磁场做匀速圆周运动的周期相同,根据偏向角的大小分析运动时间的长短.由牛顿第二定律研究轨道半径.根据圆的对称性,分析离子重新回到边界时速度方向关系和与O点距离.
解答 解: A、根据牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$
A、根据牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$
解得:r=$\frac{mv}{qB}$,
由题q、v、B大小均相同,则r相同.故A正确.
B、粒子的运动周期 T=$\frac{2πm}{qB}$,则知T相同.
根据左手定则分析可知,正离子逆时针偏转,负离子顺时针偏转,重新回到边界时正离子的速度偏向角为2π-2θ,轨迹的圆心角也为2π-2θ,运动时间t=$\frac{2π-2θ}{2π}$T.
同理,负离子运动时间t=$\frac{2θ}{2π}$T,显然时间不等.故B错误.
C、正负离子在磁场中均做匀速圆周运动,速度沿轨迹的切线方向,根据圆的对称性可知,重新回到边界时速度大小与方向相同.故C错误.
D、根据几何知识得知重新回到边界的位置与O点距离S=2rsinθ,r、θ相同,则S相同.故D正确.
故选:AD
点评 根据题意画出轨迹示意图,可根据几何关系求出回到边界时离O点的距离;利用对称关系判断回到边界时速度的方向;带电粒子在磁场中做匀速圆周运动问题求运动时间,可用关系式有t=$\frac{θ}{2π}$T,θ是轨迹的圆心角,而且轨迹的圆心角等于速度的偏转角.

练习册系列答案
相关题目
3.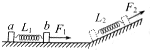 一轻弹簧两端分别连接物体a,b,在水平力作用下共同向右做匀加速运动,如图所示,在水平面上时,力为F1,弹簧长为L1,在斜面上时,力为F2,弹簧长为L2,已知a,b两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( )
一轻弹簧两端分别连接物体a,b,在水平力作用下共同向右做匀加速运动,如图所示,在水平面上时,力为F1,弹簧长为L1,在斜面上时,力为F2,弹簧长为L2,已知a,b两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( )
 一轻弹簧两端分别连接物体a,b,在水平力作用下共同向右做匀加速运动,如图所示,在水平面上时,力为F1,弹簧长为L1,在斜面上时,力为F2,弹簧长为L2,已知a,b两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( )
一轻弹簧两端分别连接物体a,b,在水平力作用下共同向右做匀加速运动,如图所示,在水平面上时,力为F1,弹簧长为L1,在斜面上时,力为F2,弹簧长为L2,已知a,b两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( )| A. | $\frac{{L}_{1}+{L}_{2}}{2}$ | B. | $\frac{{F}_{1}{L}_{1}-{F}_{2}{L}_{2}}{{F}_{2}-{F}_{1}}$ | ||
| C. | $\frac{{F}_{2}{L}_{1}-{F}_{1}{L}_{2}}{{F}_{2}-{F}_{1}}$ | D. | $\frac{{F}_{2}{L}_{1}+{F}_{1}{L}_{2}}{{F}_{2}+{F}_{1}}$ |
1.据报道,2009年4月29日,美国亚利桑那州一天文观测机构发现一颗与太阳系其它行星逆向运行的小行星,代号为2009HC82.该小行星绕太阳一周的时间为N年,直径2~3千米,其轨道平面与地球轨道平面呈155°的倾斜.假定该小行星与地球均以太阳为中心做匀速圆周运动,则小行星和地球绕太阳运动的速度大小的比值为( )
| A. | N${\;}^{-\frac{1}{3}}$ | B. | N${\;}^{-\frac{1}{2}}$ | C. | N${\;}^{\frac{3}{2}}$ | D. | N${\;}^{\frac{2}{3}}$ |
8.关于热现象,下列说法正确的是( )
| A. | 布朗运动就是液体分子的运动 | |
| B. | 自然界中进行的涉及热现象的宏观过程都具有方向性 | |
| C. | 气体吸收热量,内能一定增加 | |
| D. | 气体压强是由气体重力产生的 |
18.一列简谐横波沿x轴正方向传播,在x=2m处的质点的振动图象如图1所示,在x=8m处的质点的振动图象如图2所示.下列说法正确的是( )


| A. | 该波的周期为12s | |
| B. | x=2m处的质点在平衡位置向+y方向振动时,x=8m处的质点在波峰 | |
| C. | 在0~4s内x=2m处和x=8m处的质点通过的路程均为6cm | |
| D. | 该波的波长可能为8m | |
| E. | 该波的传播速度可能为2m/s |
5.已知质量分布均匀的球壳对其内部物体的引力为零,设想在地球赤道正上方高h处和正下方深为h处各修建一绕地心的环形真空轨道,轨道面与赤道面共面,两物件分布在上述两轨道中做匀速圆周运动,轨道对它们均无作用力,设地球半径为R,则( )
| A. | 两物体的速度大小之比为$\frac{R}{{R}^{2}-{h}^{2}}$$\sqrt{(R+h)R}$ | |
| B. | 两物体的速度大小之比为$\frac{R}{{R}^{2}-{h}^{2}}$$\sqrt{Rh}$ | |
| C. | 两物体的加速度大小之比为$\frac{{R}^{3}}{(R+h)^{2}(R-h)}$ | |
| D. | 两物体的加速度大小之比为$\frac{R+h}{R-h}$ |
2. 我国嫦娥探月计划实施以来,已成功发射“嫦娥”一号、“嫦娥”二号、“嫦娥”三号 飞船.“嫦娥”二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.2011年8月,“嫦娥二号”成功进入了环绕“日地拉格朗日”点的轨道,我国成了造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,“嫦娥二号”处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动.则“嫦娥二号”的( )
我国嫦娥探月计划实施以来,已成功发射“嫦娥”一号、“嫦娥”二号、“嫦娥”三号 飞船.“嫦娥”二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.2011年8月,“嫦娥二号”成功进入了环绕“日地拉格朗日”点的轨道,我国成了造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,“嫦娥二号”处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动.则“嫦娥二号”的( )
 我国嫦娥探月计划实施以来,已成功发射“嫦娥”一号、“嫦娥”二号、“嫦娥”三号 飞船.“嫦娥”二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.2011年8月,“嫦娥二号”成功进入了环绕“日地拉格朗日”点的轨道,我国成了造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,“嫦娥二号”处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动.则“嫦娥二号”的( )
我国嫦娥探月计划实施以来,已成功发射“嫦娥”一号、“嫦娥”二号、“嫦娥”三号 飞船.“嫦娥”二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.2011年8月,“嫦娥二号”成功进入了环绕“日地拉格朗日”点的轨道,我国成了造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,“嫦娥二号”处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动.则“嫦娥二号”的( )| A. | 周期等于地球自转周期 | B. | 线速度大于地球的线速度 | ||
| C. | 向心加速度大于地球的向心加速度 | D. | 向心力仅由太阳提供 |
3. 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103 kg,汽车受到地面的阻力为车重的0.1倍,取g=10m/s2,则下列说法不正确的是( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103 kg,汽车受到地面的阻力为车重的0.1倍,取g=10m/s2,则下列说法不正确的是( )
 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103 kg,汽车受到地面的阻力为车重的0.1倍,取g=10m/s2,则下列说法不正确的是( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持额定功率运动,其v-t图象如图所示.已知汽车的质量为m=2×103 kg,汽车受到地面的阻力为车重的0.1倍,取g=10m/s2,则下列说法不正确的是( )| A. | 汽车在前5秒内的牵引力为4×103 N | B. | 汽车在前5秒内的牵引力为6×103 N | ||
| C. | 汽车的额定功率为60 kW | D. | 汽车的最大速度为30 m/s |
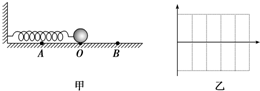 如图甲所示的弹簧振子,放在光滑有水平桌面上,O是平衡位置,弹簧振子在AB间做简谐运动,AB间的距离为6cm,已知A到B的最短时间为0.1s.
如图甲所示的弹簧振子,放在光滑有水平桌面上,O是平衡位置,弹簧振子在AB间做简谐运动,AB间的距离为6cm,已知A到B的最短时间为0.1s.