题目内容
如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道,若小球在两圆轨道的最高点对轨道的压力都恰好为零,试求CD段的长度。

【解析】设小球通过C点时的速度为vC,通过甲轨道最高点的速度为v1,根据小球对轨道压力为零,
有![]() ①(2分)
①(2分)
取轨道最低点所在水平面为参考平面,由机械能守恒定律有
![]() ②(3分)
②(3分)
联立①②式,
可得![]() (1分)
(1分)
设小球通过D点的速度为vD,通过乙轨道最高点的速度为v2,
则有:![]() ③(2分)
③(2分)
取轨道最低点所在水平面为参考平面,由机械能守恒定律有:
![]() ④(3分)
④(3分)
联立③④式,
可得![]() (1分)
(1分)
设CD段长度为l,对小球通过CD段的过程,由动能定理有:
![]() (3分)
(3分)
解得:![]() (1分)
(1分)
答案:![]()
【总结提升】机械能守恒定律应用三要点
(1)正确选取研究对象,必须明确机械能守恒定律针对的是一个系统,而不是单个物体。
(2)灵活选取零势能位置,重力势能常选最低点或物体的初始位置为零势能位置,弹性势能选弹簧原长为零势能位置。
(3)运用机械能守恒定律解题的关键在于确定“一个过程”和“两个状态”。所谓“一个过程”是指研究对象所经历的力学过程,了解研究对象在此过程中的受力情况以及各力的做功情况;“两个状态”是指研究对象在此过程中的开始和结束时所处的状态,找出研究对象分别在初状态和末状态的动能和势能。

 发散思维新课堂系列答案
发散思维新课堂系列答案 如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一个小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道,若小球在两圆轨道的最高点对轨道的压力都恰好为零.
如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一个小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道,若小球在两圆轨道的最高点对轨道的压力都恰好为零. 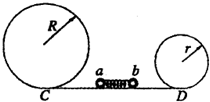 如图所示,半径分别为R和r(R>r)的甲乙两光滑圆轨道安置在同一竖直平面内,两轨道之间由一条光滑水平轨道CD相连,在水平轨道CD上一轻弹簧a、b被两小球夹住,同时释放两小球,a、b球恰好能通过各自的圆轨道的最高点,求:
如图所示,半径分别为R和r(R>r)的甲乙两光滑圆轨道安置在同一竖直平面内,两轨道之间由一条光滑水平轨道CD相连,在水平轨道CD上一轻弹簧a、b被两小球夹住,同时释放两小球,a、b球恰好能通过各自的圆轨道的最高点,求: (2011?信阳二模)如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,又滑上乙轨道,最后离开两圆轨道.通过动摩擦因数为μ的CD段,若小球在两圆轨道的最高点对轨道压力都恰好为零,且CD段的动摩擦因数为μ,试求水平CD段的长度.
(2011?信阳二模)如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,又滑上乙轨道,最后离开两圆轨道.通过动摩擦因数为μ的CD段,若小球在两圆轨道的最高点对轨道压力都恰好为零,且CD段的动摩擦因数为μ,试求水平CD段的长度.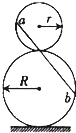 如图所示,半径分别为r和R的圆环竖直叠放(相切)于水平面上,一条公共斜弦过两圆切点且分别与两圆相交于a、b两点.在此弦上铺一条光滑轨道,且令一小球从b点以某一初速度沿轨道向上抛出,设小球穿过切点时不受阻挡.若该小球恰好能上升到a点,则该小球从b点运动到a点所用时间为多少?
如图所示,半径分别为r和R的圆环竖直叠放(相切)于水平面上,一条公共斜弦过两圆切点且分别与两圆相交于a、b两点.在此弦上铺一条光滑轨道,且令一小球从b点以某一初速度沿轨道向上抛出,设小球穿过切点时不受阻挡.若该小球恰好能上升到a点,则该小球从b点运动到a点所用时间为多少?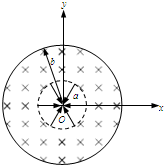 如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求:
如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求: