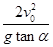��Ŀ����
��ͼ��ʾ��OΪ��ֱƽ����
Բ�������Բ�ģ�B������߸պ���ˮƽ����һ������Ϊm�Ļ��飨����Ϊ�ʵ㣩��A���ɾ�ֹ��ʼ���£������䵽�����ϵ�C�㣮��֪A�������ĸ߶�Ϊh��Բ������İ뾶ΪR���������ٶ�Ϊg������һ��Ħ������
��1�����龭B��ʱ���ٶȴ�С��
��2�����龭B��ʱ�Թ����ѹ����
��3���ڱ�֤A��λ�ò��������£��ı�Բ�����
�İ뾶����С��h�������û����A���ɾ�ֹ���£�A�㵽������ص��ˮƽ��������Ƕ��٣���ʱԲ������İ뾶�Ƕ��
| 1 |
| 4 |
��1�����龭B��ʱ���ٶȴ�С��
��2�����龭B��ʱ�Թ����ѹ����
��3���ڱ�֤A��λ�ò��������£��ı�Բ�����
�İ뾶����С��h�������û����A���ɾ�ֹ���£�A�㵽������ص��ˮƽ��������Ƕ��٣���ʱԲ������İ뾶�Ƕ��

��1�������A��B�Ĺ����У��ɻ�е���غ��mgR=
m
��� vB=
��2�����龭B��ʱ������������ʽ��N-mg=m
��� N=3mg
��ţ�ٵ�������֪�����龭B��ʱ�Թ����ѹ����СΪ3mg��������ֱ���£�
��3�������뾶Ϊr�������B�㿪ʼ��ƽ���˶�����ʱ��t��أ���h-r=
gt2
ƽ��ˮƽ���� xBC=vBt
�������A��C�����ˮƽ����Ϊ xAC=r+xBC=r+2
��r=hsin2�ȣ���AC�����ˮƽ����ΪxAC=h(sin2��+2sin��cos��)=h(
+sin2��)=
(1-cos2��+2sin2��)
��tan��=
����xAC=
[1+
sin(2��-��)]��
��Ȼ����=
+
ʱ��xAC�����ֵΪxm=
h
��ʱ r=hsin2��=h
=
h=
h
�𣺣�1�����龭B��ʱ���ٶȴ�СΪvB=
��
��2�����龭B��ʱ�Թ����ѹ��Ϊ3mg��
��3��A�㵽������ص��ˮƽ���������xm=
h����ʱԲ������İ뾶��r=
h��
| 1 |
| 2 |
| v | 2B |
��� vB=
| 2gR |
��2�����龭B��ʱ������������ʽ��N-mg=m
| ||
| R |
��� N=3mg
��ţ�ٵ�������֪�����龭B��ʱ�Թ����ѹ����СΪ3mg��������ֱ���£�
��3�������뾶Ϊr�������B�㿪ʼ��ƽ���˶�����ʱ��t��أ���h-r=
| 1 |
| 2 |
ƽ��ˮƽ���� xBC=vBt
�������A��C�����ˮƽ����Ϊ xAC=r+xBC=r+2
| r(h-r) |
��r=hsin2�ȣ���AC�����ˮƽ����ΪxAC=h(sin2��+2sin��cos��)=h(
| 1-cos2�� |
| 2 |
| h |
| 2 |
��tan��=
| 1 |
| 2 |
| h |
| 2 |
| 5 |
��Ȼ����=
| �� |
| 4 |
| �� |
| 2 |
| ||
| 2 |
��ʱ r=hsin2��=h
1-cos(
| ||
| 2 |
| 1+sin�� |
| 2 |
5+
| ||
| 10 |
�𣺣�1�����龭B��ʱ���ٶȴ�СΪvB=
| 2gR |
��2�����龭B��ʱ�Թ����ѹ��Ϊ3mg��
��3��A�㵽������ص��ˮƽ���������xm=
| ||
| 2 |
5+
| ||
| 10 |

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ʾ��BΪ��ֱԲ�������˵㣬����Բ��O����������ֱ����ļн�Ϊ����һС����Բ�������A�����ٶ�v0ƽ�ף�ǡ����B������߷������Բ�������֪�������ٶ�Ϊg����AB֮���ˮƽ����Ϊ��������
��ͼ��ʾ��BΪ��ֱԲ�������˵㣬����Բ��O����������ֱ����ļн�Ϊ����һС����Բ�������A�����ٶ�v0ƽ�ף�ǡ����B������߷������Բ�������֪�������ٶ�Ϊg����AB֮���ˮƽ����Ϊ��������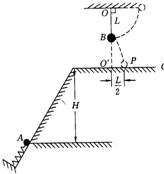 ��ͼ��ʾ����ͬһ��ֱƽ���ϣ�����Ϊ2m��С��A��ֹ�ڹ⻬б��ĵײ���б��߶�ΪH=2L��С���ܵ����ɵĵ��������ú���б�������˶����뿪б��ﵽ��ߵ�ʱ�뾲ֹ�����ڴ˴���С��B������ײ����ײ����е����ʧ����ײ����B�պ��ܰڵ�������Oͬһ�߶ȣ���A��ˮƽ������������ˮƽ��C�ϵ�P�㣬O���ͶӰO'��P��ľ���ΪL/2����֪��B����Ϊm��������L��������Ϊ�ʵ㣬�������ٶ�Ϊg�����ƿ�����������
��ͼ��ʾ����ͬһ��ֱƽ���ϣ�����Ϊ2m��С��A��ֹ�ڹ⻬б��ĵײ���б��߶�ΪH=2L��С���ܵ����ɵĵ��������ú���б�������˶����뿪б��ﵽ��ߵ�ʱ�뾲ֹ�����ڴ˴���С��B������ײ����ײ����е����ʧ����ײ����B�պ��ܰڵ�������Oͬһ�߶ȣ���A��ˮƽ������������ˮƽ��C�ϵ�P�㣬O���ͶӰO'��P��ľ���ΪL/2����֪��B����Ϊm��������L��������Ϊ�ʵ㣬�������ٶ�Ϊg�����ƿ�����������


 B��
B��
 D��
D��