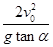题目内容
如图所示，B为竖直圆轨道的左端点，它和圆心O的连线与竖直方向的夹角为α．一小球在圆轨道左侧的A点以速度v0平抛，恰好沿B点的切线方向进入圆轨道．已知重力加速度为g，则AB之间的水平距离为（ ）分析：根据小球恰好从轨道的B端沿切线方向进入轨道，说明小球的末速度应该沿着B点切线方向，再由圆的半径和角度的关系，可以求出B点切线的方向，即平抛末速度的方向，从而可以求得竖直方向分速度，进而求出运动的时间，根据水平方向上的运动规律求出AB间的水平距离．
解答：解：
根据平行四边形定则知，小球通过B点时竖直方向上的分速度vy=v0tanθ．
则运动的时间t=
=
．
则AB间的水平距离x=v0t=
．故A正确，B、C、D错误．
故选A．
根据平行四边形定则知，小球通过B点时竖直方向上的分速度vy=v0tanθ．则运动的时间t=
| vy |
| g |
| v0tanθ |
| g |
则AB间的水平距离x=v0t=
| v02tanα |
| g |
故选A．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式灵活求解．
练习册系列答案
相关题目
B．
D．
B．
D．
B.
C.
D.
B．
D．