题目内容
（2006?淮安二模）电子自静止开始经M、N板间（两板间的电压为u）的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中，电子离开磁场时的位置P偏离入射方向的距离为L，如图所示．求匀强磁场的磁感应强度．（已知电子的质量为m，电量为e）分析：电子先经电场加速后进入磁场偏转，根据动能定理求出加速获得的速度，电子在磁场中由洛伦兹力提供向心力，根据几何知识求出轨迹半径，由牛顿第二定律求出磁感应强度．
解答：解：电子在M、N间加速后获得的速度为v，由动能定理得：
mv2-0=eu
电子进入磁场后做匀速圆周运动，设其半径为r，则：
evB=m
电子在磁场中的轨迹如图，由三角形相似得：
=
由以上三式得：B=
答：匀强磁场的磁感应强度为
．
| 1 |
| 2 |
电子进入磁场后做匀速圆周运动，设其半径为r，则：
evB=m
| v2 |
| r |
电子在磁场中的轨迹如图，由三角形相似得：
| L | ||||
|
| ||
| r |
由以上三式得：B=
| 2L |
| L2+d2 |
|
答：匀强磁场的磁感应强度为
| 2L |
| L2+d2 |
|
点评：本题是带电粒子在磁场中运动的问题，关键是画出轨迹，由几何知识求解轨迹半径．
练习册系列答案
相关题目
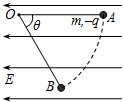（2006?淮安二模）如图所示，在场强大小为E的匀强电场中，一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球，另一端固定在O点．把小球拉到使细线水平的位置A，然后将小球由静止释放，小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零．以下说法正确的是（ ）
（2006?淮安二模）如图所示，一根不可伸长的轻绳一端拴着一个小球，另一端固定在竖直杆上，当竖直杆以角速度ω转动时，小球跟着杆一起做匀速圆周运动，此时绳与竖直方向的夹角为θ，下列关于ω与θ关系的图象正确的是（ ）