题目内容
18. 如图,一质量为m的物体B固定在轻弹簧上,弹簧下端固定在水平桌面上,弹簧原长为L.B静止时,弹簧压缩量为△L1,在B上再轻放一质量为m的物体A,A、B静止后,弹簧的弹性势能为E1;在A上施加一向下的力,使弹簧再缩短△L2,这时弹簧的弹性势能为E2.撤去向下的作用力,A、B一起向上运动.求:
如图,一质量为m的物体B固定在轻弹簧上,弹簧下端固定在水平桌面上,弹簧原长为L.B静止时,弹簧压缩量为△L1,在B上再轻放一质量为m的物体A,A、B静止后,弹簧的弹性势能为E1;在A上施加一向下的力,使弹簧再缩短△L2,这时弹簧的弹性势能为E2.撤去向下的作用力,A、B一起向上运动.求:(1)A、B一起向上运动过程中的最大速度.
(2)在A、B脱离后,物体A还能上升的高度.
分析 (1)A、B一起放在弹簧上,静止时的位置即为平衡位置,A、B一起向上运动过程中通过平衡位置的速度最大,由系统的机械能守恒求解.
(2)A、B脱离时,弹簧为原长,先由系统的机械能守恒求此时A的速度,再对A上升的过程,运用机械能守恒定律求物体A还能上升的高度.
解答 解:(1)A、B一起放在弹簧上,静止时的位置即为平衡位置,A、B一起向上运动过程中通过平衡位置的速度最大,由系统的机械能守恒得:
E2=2mg△L2+$\frac{1}{2}×2m{v}_{m}^{2}$+E1;
解得,最大速度为:vm=$\sqrt{\frac{{E}_{2}-{E}_{1}}{m}-2g△{L}_{2}}$
(2)A、B脱离时,弹簧为原长,由系统的机械能守恒得:
E2=2mg(2△L1+△L2)+$\frac{1}{2}×2m{v}^{2}$+E1;
解得,此时A的速度为:v=$\sqrt{\frac{{E}_{2}}{m}-2g(2△{L}_{1}+△{L}_{2})}$
在A、B脱离后,物体A还能上升的高度为:h=$\frac{{v}^{2}}{2g}$=$\frac{{E}_{2}}{mg}$-2(2△L1+△L2)
答:(1)A、B一起向上运动过程中的最大速度是$\sqrt{\frac{{E}_{2}-{E}_{1}}{m}-2g△{L}_{2}}$.
(2)在A、B脱离后,物体A还能上升的高度是$\frac{{E}_{2}}{mg}$-2(2△L1+△L2).
点评 解决本题的关键要明确两个物体通过平衡位置时速度最大,知道系统的机械能是守恒的,但对单个物体来说,机械能并不守恒.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
10.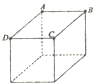 在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
 在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )| A. | $\sqrt{2}$N | B. | 2$\sqrt{2}$N | C. | 3.6$\sqrt{2}$N | D. | 3.6$\sqrt{3}$N |
7.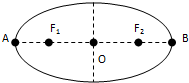 某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )
某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )
 某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )
某行星绕太阳运行的椭圆轨道如图所示.F1和F2是椭圆的两个焦点,行星在A点的速率比在B点的速率大,则太阳位于( )| A. | F1点 | B. | F2点 | C. | O点 | D. | 均不正确 |




 甲同学在家里做用单摆测定重力加速度的实验,但没有合适的摆球.他找到了一个儿童玩具弹力小球,其直径大小约为2cm左右,代替实验用小球.他设计的实验步驟如下:
甲同学在家里做用单摆测定重力加速度的实验,但没有合适的摆球.他找到了一个儿童玩具弹力小球,其直径大小约为2cm左右,代替实验用小球.他设计的实验步驟如下: 当前“雾霾”成为全社会关注的热点,为了缓解空气污染,我国多地市启动了“光伏工程”示范项目,在屋顶安装太阳能光伏板,如图所示是某中学的教学楼顶安装了总功率为20kW的光伏发电系统.按一天的有效光照时间8h计算,该中学光伏发电系统一天共发电160kw•h,这些发电量如果由热电转换效率为30%的热电厂来完成,需要燃烧64kg煤;你一定很关注“雾霾天气”的报道,请结合所了解的知识,谈谈家庭光伏发电的优点:减少污染、节约能源(谈一点即可).(煤的热值q煤=3.0×107J/kg )
当前“雾霾”成为全社会关注的热点,为了缓解空气污染,我国多地市启动了“光伏工程”示范项目,在屋顶安装太阳能光伏板,如图所示是某中学的教学楼顶安装了总功率为20kW的光伏发电系统.按一天的有效光照时间8h计算,该中学光伏发电系统一天共发电160kw•h,这些发电量如果由热电转换效率为30%的热电厂来完成,需要燃烧64kg煤;你一定很关注“雾霾天气”的报道,请结合所了解的知识,谈谈家庭光伏发电的优点:减少污染、节约能源(谈一点即可).(煤的热值q煤=3.0×107J/kg ) 如图是一个带正电的点电荷周围的电场线.
如图是一个带正电的点电荷周围的电场线.