题目内容
10．
如图所示，将一质量为m的滑块放在水平地面上，滑块与水平地面之间的动摩擦因数为μ，现将滑块与一轻弹簧相连，弹簧另一端拴接在竖直的墙壁上，开始弹簧处于原长状态，此时的滑块位于O点，现向右缓慢拉滑块到M点，此过程中拉力对滑块所做的功为W，然后将滑块无初速释放，滑块经O点向左运动到N点时速度减为零，已知MN=L，重力加速度为g．滑块在M、N两点时弹簧的弹性势能分别为EpM、EpN．则下列说法正确的是（ ）| A． | EpM＞EpN | |
| B． | 当弹簧处于原长时滑块的速度最大 | |
| C． | EpN＞W-$\frac{3}{2}$μmgL | |
| D． | 当滑块运动到O点时，滑块的动能一定小于W-μmgL |
分析 滑块向左运动的过程中，弹簧的弹性势能转化为内能．当滑块的合力为零时速度最大．根据能量守恒定律求出N点的弹性势能．并求出滑块运动到O点的动能．
解答 解：A、滑块从M运动到N时，弹簧的弹性势能转化为内能，则EpM＞EpN．故A正确．
B、滑块向左运动时，弹簧的弹力先大于摩擦力，后小于摩擦力，先加速后减速，所以当弹力与摩擦力大小相等、方向相反时速度最大，此时弹簧处于拉伸状态，故B错误．
C、滑块从M运动到N时，由能量守恒定律有：
EpM=EpN+μmgL…①
滑块从O到M的过程，有：W=EpM+μmg$\overline{OM}$…②
由于EpM＞EpN，则有：$\overline{OM}$＞$\overline{ON}$…③
即有 $\overline{OM}$＞$\frac{L}{2}$…④
由①②④解得：EpN＜W-$\frac{3}{2}$μmgL，故C错误．
D、滑块从M运动到O的过程，由能量守恒定律有：
EKO+μmg$\overline{OM}$=EpM…⑤
则得滑块运动到O点时的动能为：EKO=EpM-μmg$\overline{OM}$=W-2μmg$\overline{OM}$…⑥
将 $\overline{OM}$＞$\frac{L}{2}$代入⑥得 EKO＜W-μmgL．故D正确．
故选：AD
点评 解决本题的关键要准确把握能量是如何转化的，分段运用能量守恒定律列式分析．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
一根两端开口、横截面积为S=2cm2的足够长玻璃管竖直插入水银槽中并固定（插入水银槽中的部分足够深）．管中有一个质量不计的光滑活塞，活塞下封闭着温度t1=7℃，长度L1=21cm的气柱．已知环境大气压恒为p0=1.02×105Pa，水银密度ρ=13.6×103kg/m3．（g取10m/s2）
5．
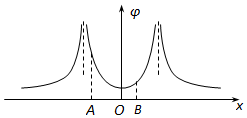某静电场在x轴上各点的电势φ随坐标x的分布图象如图，x轴上A、O、B三点的电势值分别为φA、φO、φB，电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx，电子在A、O、B三点的电势能分别为EPA、EPO、EPB，下列判断正确的是（ ）
某静电场在x轴上各点的电势φ随坐标x的分布图象如图，x轴上A、O、B三点的电势值分别为φA、φO、φB，电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx，电子在A、O、B三点的电势能分别为EPA、EPO、EPB，下列判断正确的是（ ）| A． | φO＞φB＞φA | B． | EPO＜EPB＜EPA | C． | EOx＜EBx＜EAx | D． | EPO-EPA＞EPO-EPB |
如图所示，一个上下都与大气相通的直圆筒，中间用两个活塞A与B封住一定质量的理想气体，活塞面积为0.01m2．A与B都可沿圆筒无摩擦地上、下滑动，但不漏气．A的质量为M=10kg，B的质量可不计，B与一劲度系数k=2×103N/m的较长的弹簧相连，已知大气压强p0=1×105Pa，平衡时，两活塞问的距离l0=0.65m，现用力压A，使之缓慢向下移动一定距离后再次平衡，此时，用于压A的力F=2×102N，求活塞A向下移动的距离．（假定气体温度保持不变，g=10m/s2）
10．
如图，竖直放置的均匀等臂U型导热玻璃管两端封闭，管内水银封有A、B两段气柱，左管水银面高于右管水银面，高度差为h，稳定时A、B气柱的压强分别为pA和pB，则（ ）
如图，竖直放置的均匀等臂U型导热玻璃管两端封闭，管内水银封有A、B两段气柱，左管水银面高于右管水银面，高度差为h，稳定时A、B气柱的压强分别为pA和pB，则（ ）| A． | 若环境温度升高，pA增大，pB减小 | |
| B． | 若环境温度降低，稳定后AB气柱的压强比值增大 | |
| C． | 若环境温度升高，稳定后AB气柱压强变化△pA一定小于△pB | |
| D． | 若环境温度降低，稳定后A处液面高度变化△h可能大于$\frac{h}{2}$ |
7．
在同一平直公路上有A、B两辆汽车，它们的v-t图象分别为a、b，如图所示，a线平行于时间轴，b线为过原点的倾斜直线，根据图象可知（ ）
在同一平直公路上有A、B两辆汽车，它们的v-t图象分别为a、b，如图所示，a线平行于时间轴，b线为过原点的倾斜直线，根据图象可知（ ）| A． | A车静止，B车做匀速直线运动 | |
| B． | A车静止，B车做匀加速直线运动 | |
| C． | A车做匀速直线运动，B车做匀加速直线运动 | |
| D． | A车做匀速直线运动，B车做匀速直线运动 |
