题目内容
 (2003?上海)如图所示,OACO为置于水平面内的光滑闭合金属导轨,O、C处分别接有短电阻丝(图中
(2003?上海)如图所示,OACO为置于水平面内的光滑闭合金属导轨,O、C处分别接有短电阻丝(图中粗线表法),R1=4Ω、R2=8Ω(导轨其它部分电阻不计).导轨OAC的形状满足方程y=2sin(
| π | 3 |
(1)外力F的最大值;
(2)金属棒在导轨上运动时电阻丝R1上消耗的最大功率;
(3)在滑动过程中通过金属棒的电流I与时间t的关系.
分析:金属棒在导轨上从O点滑动到C点,切割磁感线产生电动势,有效切割长度y按正弦规律变化,当y最大时,感应电流最大,安培力最大,外力F最大.电阻丝R1上消耗的功率最大.本题根据法拉弟定律、欧姆定律等规律求解.
解答:解:(1)金属棒匀速运动 F=F安
ε=BLv①
I=
F=BIL=
又Lmax=2sin
=2(m)
=
Ω
故Fmax=0.22×22×5.0×
N=0.3N
(2)P1=
=1W
(3)金属棒与导轨接触点间的长度随时间变化 L=2sin(
x)(m)
且 x=vt,E=BLv,
得到I=
=
=2sin(
vt)=
sin(
t)(A)
答:(1)外力F的最大值0.3N;
(2)金属棒在导轨上运动时电阻丝R1上消耗的最大功率为1W;
(3)在滑动过程中通过金属棒的电流I与时间t的关系为
sin(
t)A.
ε=BLv①
I=
| E |
| R总 |
F=BIL=
| B2L2v |
| R总 |
又Lmax=2sin
| π |
| 2 |
| R1R2 |
| R1+R2 |
| 8 |
| 3 |
故Fmax=0.22×22×5.0×
| 3 |
| 8 |
(2)P1=
| E2 |
| R1 |
(3)金属棒与导轨接触点间的长度随时间变化 L=2sin(
| π |
| 3 |
且 x=vt,E=BLv,
得到I=
| ε |
| R总 |
| Bv |
| R总 |
| π |
| 3 |
| 3 |
| 4 |
| 5π |
| 3 |
答:(1)外力F的最大值0.3N;
(2)金属棒在导轨上运动时电阻丝R1上消耗的最大功率为1W;
(3)在滑动过程中通过金属棒的电流I与时间t的关系为
| 3 |
| 4 |
| 5π |
| 3 |
点评:本题中导线的有效切割长度随时间作正弦规律变化,产生正弦式交变电流,提供了一种产生正弦式交变电流的一种方式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2003?上海)如图所示,在“有固定转动轴物体的平衡条件实验中,调节力矩盘使其平衡,弹簧秤的读数为
(2003?上海)如图所示,在“有固定转动轴物体的平衡条件实验中,调节力矩盘使其平衡,弹簧秤的读数为 (2003?上海)如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2).某同学对此题的解法为:小球沿斜面运动,则
(2003?上海)如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2).某同学对此题的解法为:小球沿斜面运动,则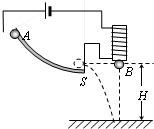 (2003?上海)如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两球总是同时落地,该实验现象说明了A球在离开轨道后
(2003?上海)如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两球总是同时落地,该实验现象说明了A球在离开轨道后